Bis za karę
Sześcienne sudoku zamieszczone w poprzednim wpisie nie było, jako typ zadania – wbrew moim przypuszczeniom – nowinką. Raczej reaktywacją lub retro nowinką. Po krótkiej kwerendzie ustaliłem, że debiutowało w japońskim magazynie Puzzler przed 14 laty. Pamięć zawiodła mnie tym bardziej, że ta odmiana pojawiła się na pierwszych mistrzostwach świata w Lukce w 2006 roku, a później gościła czasem na różnych zawodach i turniejach dla sudokomanów.
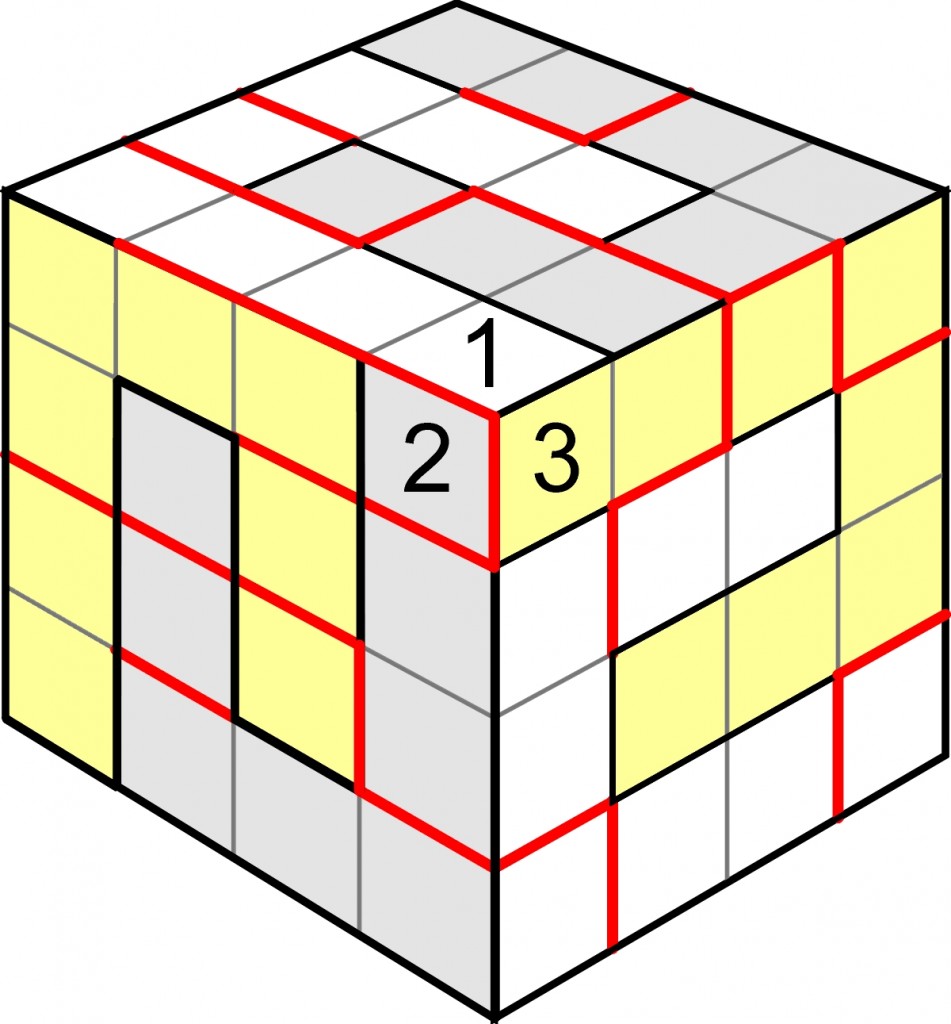
Postanowiłem ukarać się za niefortunną „nowinkę” w osobliwy sposób, zamieszczając jeszcze jedno sześcienne sudoku, ale bardziej zakręcone – takie, którego nikt nie rozwiąże, więc będzie mi smutno z powodu braku komentarzy z rozwiązaniem 🙂 .
Dokładnych zasad zabawy nie podaję. Ogólne są podobne do zamieszczonych w poprzednim wpisie, a co jeszcze trzeba uwzględnić, pozostawiam domyślności szanownych gości. Wszystko po to, aby była większa szansa, że rozwiązania się nie pojawią, czyli nikt nie poda, w ilu miejscach stykają się rogami pola z taką samą cyfrą.

Komentarze
Zadanie łatwe. Takich miejsc jest trzynaście.
Warstwami od góry
41523876
24638715
35786142
86175423
Na górnej powierzchni
1784
5836
6325
7241
Dodatkowy warunek
Między dwoma liczbami różnymi o 1 jest czerwona kreska.
Prawdopodobnie oczekiwaną odpowiedzią jest: 13.
Trudniej było sprawdzić, że po usunięciu z sześcianu wszystkich cyfr pojawi się więcej niż jedno rozwiązanie.
w czterech miejscach 🙂
ok.. strzelałem 😉
Mam nadzieje ze Pan nie zartowal z trudnoscia tego zadania (dziala to na mnie jak plachta na byka 😉 ) , poniewaz satysfakcja nie bedzie tak duza jezeli moje rozwiazanie okaze sie poprawne: 8 roznych cyfr nalezy wpisac w trzech wzajemnie prostopadlych plaszczyznach we wszystkich rzedach, rowniez w polach jasnoszarym, ciemnoszarym, zoltym nalezy wpisac 8 roznych znakow, czerwone linie oddzielaja pola w ktorych roznica cyfr wynosi 1.Takie same cyfry „po skosie” sasiaduja w 10 miejscach. Rozwiazanie raczej jest jednoznaczne, wiec przypuszczam ze jest poprawne (co najwyzej nie recze za poprawnosc przeliczenia sasiadujacych cyfr – pora juz pozna) 🙂 pozdrawiam
Dzisiaj naliczyłem 11 takich miejsc, ale jak w pracy znajdę chwilę, to nabiorę pewności 🙂
Trzy wpisy i dwie błędne odpowiedzi…
Teraz już musi być dobrze: rozwiązałem zadanie po raz drugi, sądzę, że rozwiązanie, z podanymi przeze mnie regułami, jest jedno.
Pola z takimi samymi cyframi stykają się w 12 miejscach.
PS: można jeszcze dopisać warunek, który wcale nie musi być oczywisty, że jeżeli pola nie są oddzielone czerwoną krawędzią, to różnica sąsiadujących cyfr musi być większa od 1.
W powyższym zadaniu, jeżeli nie uwzględni się tego warunku, szybko dochodzi się do sprzeczności (przynajmniej w połowie rozwiązywania), ale bez większego problemu dałoby się stworzyć „podstępne” zadanie, gdzie by tak nie musiało być.
Ach, co za gapa ze mnie…
Już miałem wszystkie miejsce na rysunku zaznaczone, a i tak zapomniałem trzy ósemki policzyć jako dwa miejsca…
Prawidłowa odpowiedź to oczywiście 13 🙂 czyli jednak 4 wpisy i trzy błędne odpowiedzi…
Przyznam, że zadania „dedukcyjne” bardzo przypadły mi do gustu 🙂 można poćwiczyć nie tylko logikę, ale i kreatywność.
Pozdrawiam 🙂
Dodatkowo liczby oddzielone czerwoną linią muszą być kolejne.
13 razy stykają się pola z taką samą cyfrą.
13.
W trzynastu miejscach.
Trudno bardziej zdopingować czytelników do pracy…
Wpisujemy 8 cyfr, różnych w rzędach i kolumnach oraz 8-polowych „zawijasach”. Cyfry oddzielone czerwona kreską różnią się o jeden.
Zagadka niezbyt trudna (1, 2 i 3 wpisuje się wszystkie „od ręki”, a potem trzeba chwilkę pomyśleć i znowu wpisywać „jak leci”)
Doliczyłem się 13-stu miejsc.
Moim zdaniem zadanie nie należy do zbyt trudnych.
http://img838.imageshack.us/img838/9043/9eg2.jpg
Aha, ja naliczyłem 12, ale upewniłem się dopiero po piątym liczeniu 🙂
Jak widać liczenie było najtrudniejszym zadaniem. Wychodziło za każdym razem 12, ale aż tylu nie mogło się mylić! Liczę znowu i nadal 12:) Aż w końcu jest!!!! Jest 13!!! 🙂