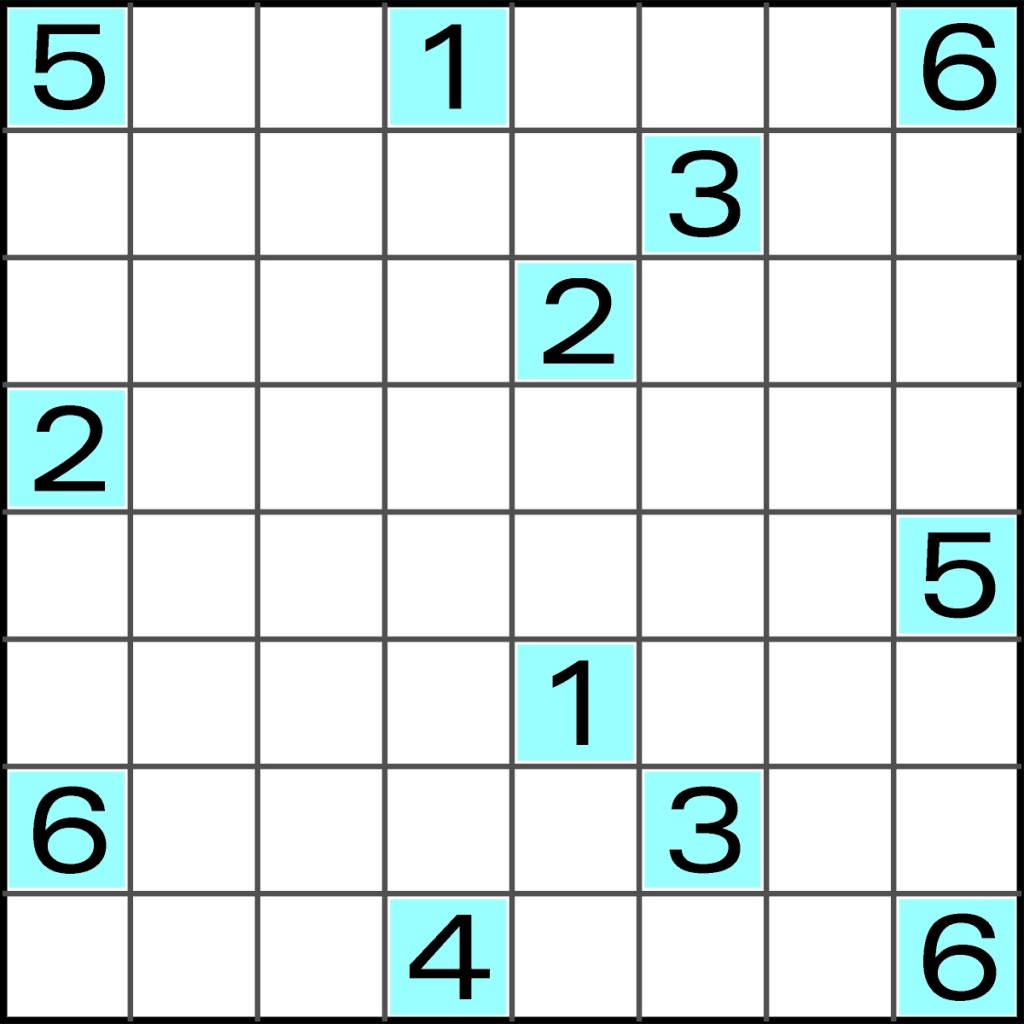
Łamane inaczej
Niemal we wszystkich wariantach zadań zwanych mackami linie zaczynające się od liczb sięgają:
(a) wszystkich pól diagramu,
(b) każdego pola tylko raz.
Inaczej mówiąc, suma liczb w diagramie równa jest liczbie wolnych pól.
W poniższej odmianie warunek (a) nie jest spełniony – wolnych pól jest więcej, niż wynosi suma liczb, więc niektóre pozostają „niemacane”.
Każda liczba wysuwa jedną mackę, sięgającą tylu pól, jaka jest wartość liczby. Macka może być linią łamaną, ale wówczas tworzące ją odcinki muszą być różnej długości, a ściślej – każdy z nich powinien łączyć inną liczbę pól, jak w przypadku 3, 4, i 7 w poniższym przykładzie.
Odcinek wychodzący z liczby zawsze łączy co najmniej dwa pola – to z liczbą i następne.
Przy „mackowaniu” najtrudniejszy jest początek, czyli znalezienie pierwszego pewniaka.
W rozwiązaniu wystarczy podać, ilu pól na przekątnych sięgają macki i jaka jest suma liczb sięgających mackami tych pól.


Komentarze
Dobrze jest zacząć od prawego dolnego rogu 🙂
Macki sięgają 10 z 13 pól na przekątnych, a suma liczb sięgających mackami tych pól wynosi 43.
Pozdrawiam 🙂
„ściślej ? każdy z nich powinien łączyć inną liczbę pól”
Jeżeli popatrzymy przykładowo na trójkę to dwa odcinki łączą taką samą liczbę pól (równą 2).
Czy sumowanie pól liczy się na całej długości odcinka – i w przykładzie jest błąd – czy jeżeli macka wychodząca ze swojego źródła zaznaczy już dwa pola to przy łamaniu w tym polu nie uwzględnia się kolejnej części macki (w trójce by to było: 2 pola, 1 pole)?
Odpowiedź pod komentarzem Wiąza (właściwie powinna być pod tym, ale sprawa jest podobna).
mp
Drobne uściślenie:
macka ma sięgać środka pola, brzegu pola? Powiedzmy, że zakończę mackę po dotarciu do brzegu jakiegoś pola (de facto pola będą połączone, jak dotrę do ścianki pola) i mogłoby to spowodować, że macki będą równe lub nie, jeśli będzie mi to akurat pasować. Tak na prawdę mackę mogę zakończyć w dowolnym miejscu pola, co będzie w zgodzie z instrukcją.
Oczywiście rysunek wyjaśnia, gdzie mam zakończyć mackę ( w środku pola) i pierwsza macka będzie miała długość x+0,5 kratki, ale instrukcja każe mi tylko pomacać pola:)
Jeśli się dobrze przyjrzeć (po kliknięciu na rysunek), to macka wychodząca z pola z cyfrą sięga „ciutek” poza brzeg tego pola, więc łączy to pole z następnym. A zatem pierwszy z odcinków macki wychodzącej z trójki łączy trzy pola, a drugi dwa.
mp
Zadanie ciekawsze i trudniejsze niż to z poprzedniego wpisu.
http://pokazywarka.pl/a54s6f/
Macki nie sięgają 3 pól na przekątnych.
Suma mi wyszła 32 (licząc bez krotności).
Będę panie Marku upierdliwy, ale tylko dla samej przyjemności dyskusji. Skoro sam pan zauważył, że macka łączy także pole z liczbą, to tym samym liczba ta nie odzwierciedla liczby pól połączonych macką. Wniosek z pana komentarza:
” A zatem pierwszy z odcinków macki wychodzącej z trójki łączy trzy pola, a drugi dwa.”:
dana macka łączy 4 pola, a nie 3.
😀
Powiedziałbym tak:
1) dwie macki nie mogą „macać” tego samego pola, ale dwa odcinki tej samej macki – i owszem
2) pole z którego wychodzi macka, nie jest przez nią „macane”, ale jest łączone macką z następnym polem i ewentualnie kolejnymi
Summa summarum: 3+2-1-1=3
Może trochę naciągam, ale jakoś muszę się ratować 🙂
mp
http://img835.imageshack.us/img835/7977/ai21024x1024.jpg
Punkt nr 2 z wyjaśnienia, bardzo przypadł mi do gustu 🙂
A ja stanę w obronie pana Marka:
liczba w polu informuje ilu pól SIĘGA macka, a odcinki łamanej powinny ŁĄCZYĆ różną ilość pól.
W rozwiązywaniu sprowadza się to do tego, że ilość łączonych pól jest zawsze o 1 większa od liczby pól, których dosięga macka.
Wydaje mi się, że to bardzo podobny problem jak w przypadku tradycyjnych urządzeń pomiarowych: za oknem mamy 22 st. C, ale 23 kreski od zera, 15mm to 16 kresek etc.
@GPSe: „Wydaje mi się, że to bardzo podobny problem jak w przypadku tradycyjnych urządzeń pomiarowych: za oknem mamy 22 st. C, ale 23 kreski od zera, 15mm to 16 kresek etc.”
Wiadomo o co chodzi, ale tak dla dalszej zabawy: 22 st. C to jednak 22 kreski od zera (zależy co przez ‚od zera’ rozumiemy), choć mój termometr ma ich więcej, znacznie więcej, pomijam tu linijkę, mam taką z kreskami co półmilimetra 🙂 No i nie miszajmy tu miary długości/temepratury z miarą liczności elementów (kresek) co ma się nijak to tego.
Całe to moje bicie piany :):) spowodowało tłumaczenie p.Marka:
„Jeśli się dobrze przyjrzeć (po kliknięciu na rysunek), to macka wychodząca z pola z cyfrą sięga ?ciutek? poza brzeg tego pola…” co daje ogromne pole do ‚nadużycia’ w rozwiązywaniu tego zadania, jeśli będziemy mierzyć długość odcinków macki zamiast liczby połączonych pól. 😀
Macki sięgają 10 pól na przekątnych. Suma liczb wypuszczających te macki to 38.
Rys: http://bankfotek.pl/view/1492966
wliczając liczby będące źródłem macek, pól na przekątnych jest oczywiście 13.
Pozdrawiam
http://s1.pokazywarka.pl/i/2007877/620976/lamane-inaczej.jpg
I przekątna=0+5+5+6+1+6=23
II =3+2+5+0+4+6+0=20
@Wiaz: a mnie sie wydaje ze to wlasnie nie pozostawia pola do naduzyc 😉 lamana na poczatku zawsze jest o pol jednostki dlugosci boku pola dluzsza 😉 przykladowo macka od 7 sklada sie z odcinkow o dlugosciach: 1,5 ; 4 ; 1.
Mozna by to oczywiscie dokladnie opisac: macka wychodzac z pola z liczba przebiega dodatkowa dlugosc od boku do srodka, macka moze siegnac co najwyzej do srodka ktoregos z pol, dlugosc odcinkow lamanych mierzymy tak i tak…
Mnie osobiscie zadanie sformulowane tak jak teraz wydaje sie scisle w wystarczajacym stopniu.
Pozdrawiam 🙂