Klepki

30 kwietnia 2013
Marek Penszko

Czego to ludzie nie wymyślą, żeby… myśleć. Tak sobie myślę, przeglądając strony z wariacjami na temat sudoku. Niewielkich modyfikacji tej łamigłówki jest blisko setka, a bardziej radykalnych – zachowujących przynajmniej „szkielet”, czyli kwadrat łaciński – setki. A wszystko dlatego, że jednym sprawia przyjemność wymyślanie, a innym myślenie (przyjemnie powymyślać innym :)), choć to zabawa niszowa, żeby nie powiedzieć – elitarna.

Przechodząc do konkretów – pewien włoski wymyślacz wyszedł od fragmentu sudokowej instrukcji: „w każdym rzędzie (…) powinny znaleźć się różne cyfry” i zamiast „różne” wstawił „powtarzające się dokładnie x razy”. Tak powstały sudokowe klepki, zwane po włosku po japońsku – tatami.

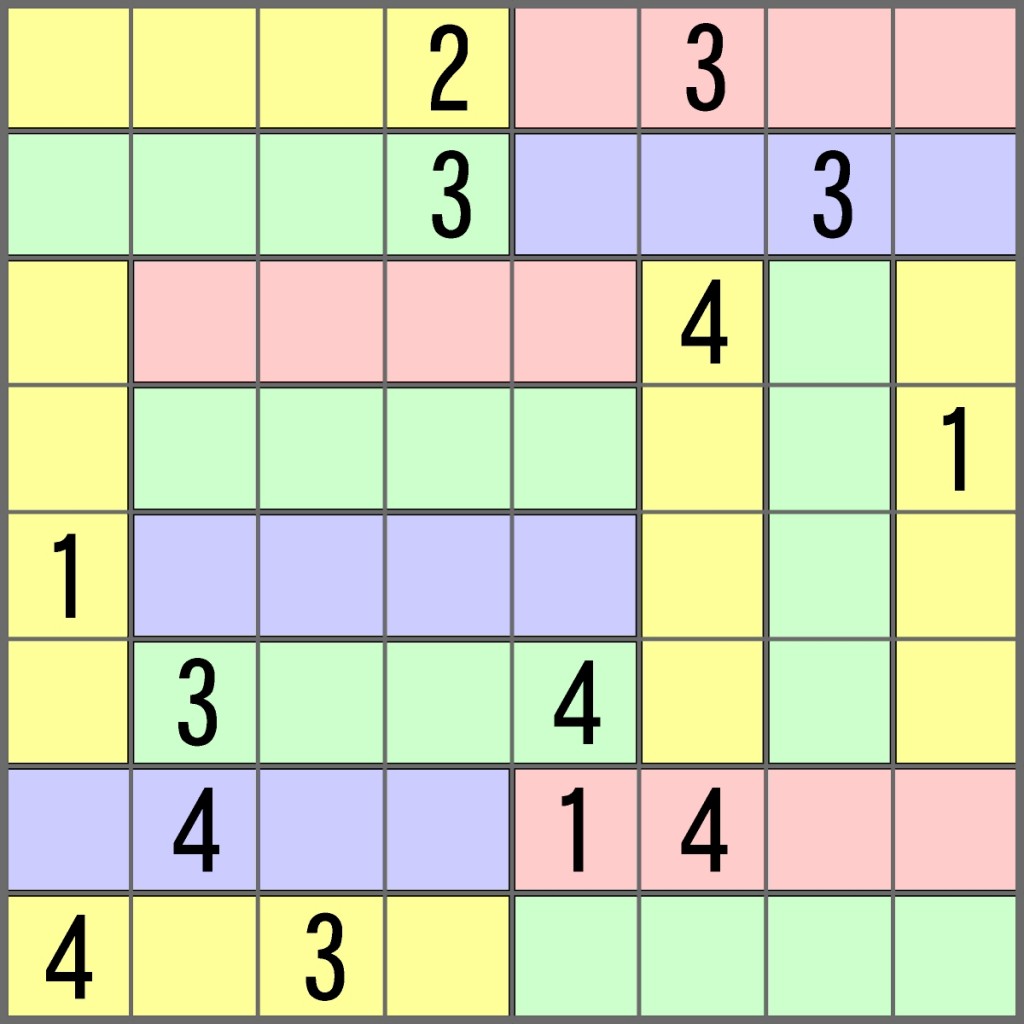
W każdej klepce powinny znaleźć się cyfry 1, 2, 3, 4. W każdym rzędzie i kolumnie diagramu również, ale w tym przypadku każda dwukrotnie. Ponadto takie same cyfry nie mogą ze sobą nigdzie sąsiadować ani w rzędach, ani w kolumnach.

Jakie cyfry pojawią się na przekątnej kolejno od lewego górnego rogu do prawego dolnego?

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co kilka dni.