Cztery stopnie

27 lipca 2012
Marek Penszko

Zadania diagramowe, kojarzące się ze schodami lub schodkami, to rzadkość. Nic dziwnego, bo pochyłość, w dodatku zębata, nie pasuje do prostokątnych stron gazet i czasopism. Kwadratowy diagram sudoku albo prostokąt krzyżówki to co innego – leżą jak ulał.

Parokrotnie w Łamiblogu gościły piramidki – np. tu i tu – które można by uznać za dwustronne schodki. Ze schodkowymi diagramami bardziej kojarzą mi się jednak dwa inne rodzaje zadań – dawny, sprzed 12 lat i całkiem nowy, tegoroczny – do obu pasuje określenie „schodki cyfrowe”.

Pierwszy pojawił się na 9. WPC w Stamfordzie w 2000 roku. W ogólnej wersji nie jest to „z natury” zadanie schodkowe, ale można je ułożyć tak, aby było – w takiej formie wygląda ładniej oraz jest merytorycznie bardziej przejrzyste, więc nic dziwnego, że organizatorzy mistrzostw także postawili na schodki:

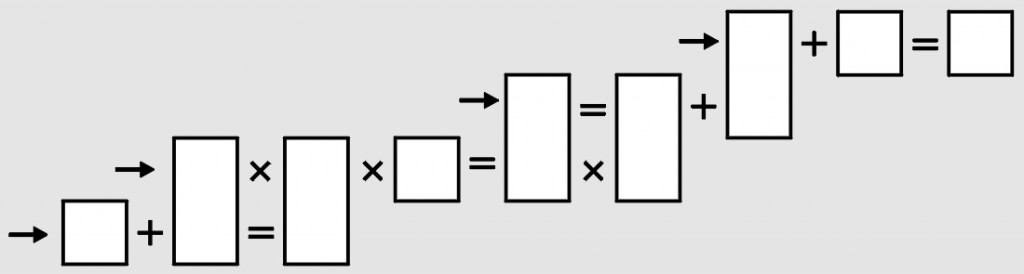
Dziewięć różnych cyfr (od 1 do 9) należy wpisać do dziewięciu pól w taki sposób, aby wskazane strzałkami równości na czterech poziomach były poprawne (cyfry w długich polach „obsługują” dwa działania).

Kiedy pierwszy raz zobaczyłem to zadanie, próbowałem je rozwiązać w głowie. Nie pamiętam, czy mi się udało, ale chyba można sobie z tym poradzić; w każdym razie warto poćwiczyć także wyobraźnię i pamięć.

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co kilka dni.