Dwukwadratura koła
Uczepiłem się cięciw i będę się ich trzymał jeszcze przez ten i może następny wpis.
Jako poligraf dyplomowany z pism drukarskich, wiem, co oznacza pojęcie dwukwadrat, chyba nieobecne nawet w Internecie. Dotyczy ono stopnia pisma i pochodzi z czasów, gdy zecerzy mozolnie składali tekst z czcionek. Onegdaj bywało też, że tym słowem określano czwartą potęgę. Zapomnijmy jednak o tych historycznych znaczeniach i nazwijmy dwukwadratem symetryczną figurę (symetria osiowa) złożoną – i tu Państwa zaskoczę 🙂 – z dwóch kwadratów. Ich wielkość nie musi być taka sama (wtedy tworzyłyby domino), ale muszą być złączone bokami:
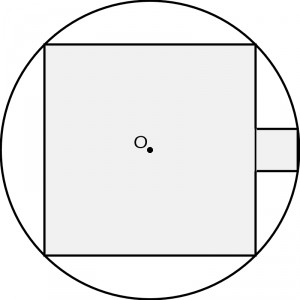
Czy na każdym dwukwadracie można opisać okrąg – tak, by na okręgu leżały przynajmniej dwa rogi jednego kwadratu i dwa drugiego? Oczywiście nie. Mniejszy kwadrat nie może być za mały w stosunku do dużego. Granicę takiej możliwości ilustruje poniższy rysunek – okrąg opisany jest na dużym kwadracie, a maluch wciska się w odcinek koła:
W takim i tylko w takim przypadku na okręgu leży sześć rogów, a ponadto cała cięciwa, którą przebiega granica między kwadratami, jest bokiem większego z nich. Gdybyśmy zaczęli konstrukcję dwukwadratu wpisanego w okrąg od tej właśnie cięciwy, to nie mogłaby być ona narysowana w odległości d od środka okręgu o promieniu r większej niż… Nietrudno policzyć. Trudniej poradzić sobie z innym zadaniem, dotyczącym bardziej ogólnego przypadku:
O ile dłuższy jest bok większego kwadratu od boku mniejszego, jeśli cięciwa, na której leży granica między bokami, znajduje się w odległości d od środka koła?
Proszę zwrócić uwagę, że promienia koła nie znamy, bowiem szukana różnica – w przeciwieństwie do samych długości boków – od promienia nie zależy.
Poza odpowiedzią mile widziane będą wszelkie informacje na temat sposobu rozwiązywania.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.



Komentarze
Z początku wydawało mi się, że naturalne (wręcz „naiwne”) podejście do tego zadania, polegające na wyznaczeniu wzorów na boki kwadratów i obliczeniu ich różnicy, doprowadzi do jakichś koszmarnie skomplikowanych obliczeń. A tu się okazało, że to jest właśnie słuszne podejście.
Oznaczmy bok dużego kwadratu jako ‚a’, a mniejszego jako ‚b’.
W dużym kwadracie nietrudno zauważyć że:
a=d+sqrt(r^2-(a/2)^2)
co można przekształcić do równania
(5/4)a^2-2da+d^2-r^2=0
delta=5r^2-d^2
Ponieważ zawsze d=4,5*r^2, czyli zawsze
sqrt(delta)>2d,
a w związku z tym jedyne dodatnie rozwiązanie tego równania to:
a=(2d+sqrt(delta))/(5/2)
W małym kwadracie:
d+b=sqrt(r^2-(b/2)^2)
co daje równanie bardzo podobne do tego z niewiadomą ‚a’:
(5/4)b^2+2db+d^2-r^2=0
o takiej samej delcie i dodatnim rozwiązaniu:
b=(-2d+sqrt(delta))/(5/2)
Po porównaniu wzorów na ‚a’ i ‚b’ dostajemy zaskakująco (przynajmniej dla mnie 🙂 ) prosty wynik
a-b=d*(8/5)
roznica wynosi 8/5 d
wykorzystujemy ow nieznany promien – oznaczajac go r,
a – bok dluzszego kwadratu, c – bok krotszego
dociagajac d do boku malego kwadratu mamy:
r^2=(c+d)^2+(c/2)^2
w duzym:
r^2=(a-d)^2+(a/2)^2
zestawiajac je ze soba i przeksztalcajac dostajemy
5/4 (a^2-c^2) = 2d(a+c)
po skroceniu przez ta sume
a-c = 8d/5
(8/5)d
Moj sposob, ogolnie mowiac, polega na oznaczeniu 2 trojkatow prostokatnych takich, ze ich boki wyrazaja sie przez dlugosci bokow dwukwadratu i promienia kola. Potem korzysta sie z twierdzenia Pitagorasa dla obu trojkatow i porownuje wartosci r^2 z obu wzorow. Z tego porownania roznica bokow trojkatow jakby sama wychodzi.
a
Oznaczmy: a – bok dużego kwadratu, b-bok małego kwadratu.
http://pokazywarka.pl/opfle8/
Stosując twierdzenie Pitagorasa dla czerwonego trójkąta mamy:
(b/2)^2+(b-d)^2=r^2
rozwiązujemy równanie kwadratowe zmiennej b i otrzymujemy:
b=2(sqrt(4d^5+5r^2)+2d)/5
Z kolei dla zielonego mamy:
(a+d)^2+(a/2)^2=r^2
Czyli:
a=2(sqrt(4d^5+5r^2)-2d)/5
Zatem szukana różnica wynosi b-a=8d/5. Jest to wielkość niezależna od promienia okręgu, co jest własnością co najmniej ciekawą.
Pozdrawiam
Mam jeszcze taki pomysł.
Opierając się na informacji szanownego autora o tym, że „szukana różnica […] od promienia nie zależy”, można rozpatrzeć przypadek graniczny zamiast ogólnego.
Wtedy obliczenia są prostsze (bo wiemy, że d=r/sqrt(2)), a dochodzi się do takiego samego rozwiązania.
Witam,
Odpowiedź: Długość boku większego kwadratu jest większa od długości boku mniejszego o 8*d/5.
Posługując sie zamieszczonym powyżej rysunkiem i oznaczając dodatkowo:
x – długość boku większego kwadratu,
y – długość boku mniejszego kwadratu,
R – promień okręgu,
zachodzą następujące związki pomiedzy d,x,R oraz d,y,R:
(x-d)^2+(x/2)^2=R^2
(y+d)^2+(y/2)^2=R^2
Odejmując powyższe równania stronami i dwukrotnie stosując zamianę różnicy kwadratów czynników na iloczyn ich sumy i różnicy:
(x+y)*(x-y-2*d)+(x+y)*(x-y)/4=0
Dzieląc powyższe równanie przez x+y, które jest oczywiście różne od zera i wprowadzając pomocniczą niewiadomą t=x-y, której w gruncie rzeczy dotyczy postawione pytanie:
t+t/4=2*d, skąd t=8*d/5
Łączę ukłony – A.S.