Kompletną drogą
Poniższy rysunek do złudzenia przypomina gumki z dwóch poprzednich wpisów. Nie zamierzam jednak „dręczyć” Państwa po raz trzeci takim samym rodzajem zadania. Tym razem chodzi, wbrew pozorom, o coś całkiem innego.
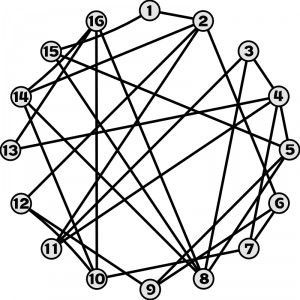
Linie oznaczają drogi łączące miasta (kółka) oznaczone kolejnymi liczbami, które należy odwiedzić. Zaczynamy od jedynki i najpierw kierujemy się ku dwójce. Jaki będzie dalszy przebieg trasy? – to właśnie trzeba ustalić, wiedząc że:
– każde miasto należy odwiedzić dokładnie raz,
– na koniec trzeba wrócić do domu, czyli zakończyć wędrówkę w jedynce.
Nie muszę chyba dodawać, że każdy odcinek między dwoma miastami powinien być prosty, czyli choć skrzyżowania są, to jakby ich nie było.
Droga jest wąska, więc nie życzę szerokiej, ale za to kompletnej.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.

Komentarze
1, 2, 12, 9, 6, 7, 10, 14, 16, 13, 4, 11, 3, 8, 5, 15, 1.
Nie rozwiązywałem zadania metodycznie – jakoś tak wyszło samo.
Pozdrawiam,
jazz
1, 2, 12, 9, 6, 7, 10, 14, 16, 13, 4, 11, 3, 8, 5, 15, 1
1-2-12-9-6-7-10-14-16-13-4-11-3-8-5-15-1
1, 2, 12, 9, 6, 7, 10, 14, 16, 13, 4, 11, 3, 8, 5, 15
To zajęło mi więcej czasu, nie miałem mądrego sposobu, więc poszedłem metodą „chybił-trafił” (ale wolę nazywać to dedukcją, bo polega na myśleniu „jeśli pójdę tą ścieżką, to następny krok musi być taki, kolejny, taki, a jeszcze dalszy taki”).
Uwzglednilem cztery mozliwosci dalszej drogi od 2. Po kazdej można wypisac kilka fragmentow trasy, a potem probowac polaczyc je w jeden cykl Hamiltona. Dosc szybko dochodzi się do tego, ze tylko po rozpoczeciu 1-2-12- da sie utworzyc cykl:
1-2-12-9-6-7-10-14-16-13-4-11-3-8-5-15-1
a