2,5,10
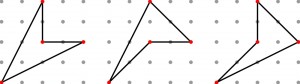
Jeżeli trójkąt straci boki, a pozostaną wierzchołki, to jego rekonstrukcja będzie trywialna. W przypadku czworokąta sprawa nie jest już taka prosta, bo jednoznaczna tylko wówczas, gdy czworokąt jest wypukły. Dla wklęsłego są trzy możliwości:
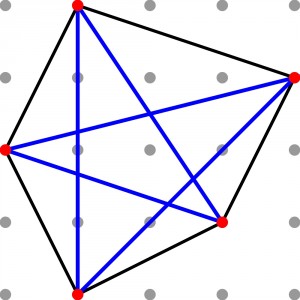
Więcej niejednoznaczności pojawia się dla pięciokąta, włącznie z na pozór kuriozalną sytuacją:
dwa pięciokąty „wsparte” na tych samych wierzchołkach mogą nie mieć żadnego wspólnego boku.
Czy potrafią Państwo wskazać 5 punktów z układu 16 poniżej, które będą wierzchołkami takich właśnie dwóch pięciokątów – bez pokrywających się boków – i narysować (nazwać) te pięciokąty.
Wykluczamy oczywiście figury z przecinającymi się bokami, których skrajnym przypadkiem są tzw. wielokąty gwiaździste:
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.


Komentarze
na przykład:
a1-d1-b2-c2-b4
i
a1-b2-b4-d1-c2
hmmm, ale nazwać ich nie potrafię.
Nazwy tworzą właśnie podane współrzędne wierzchołków.
mp
Jedyny wniosek, to taki, że 3 dowolne punkty nie mogą leżeć na tej samej prostej.
Pięciokąt nr 1:
a4-c3-b2-d3-b1-a4
Pięciokąt nr 2:
a4-d3-c3-b1-b2-a4
Trudne.
Punkty to np.: a4,b1,b2,c3,d3 (można otrzymać 4 takie zestawy)
Jeden z pięciokątów otrzymamy łącząc następująco: a4-b1-b2-d3-c3-a4.
Drugi a4-d3-b1-c3-b2-a4
Pierwszy pięciokąt: 1a-4b-2c-1d-2b-1a
Drugi pięciokąt: 1a-2c-2b-4b-1d-1a
Bardzo przyjemne zadanie 🙂
Proponuję: a4 – a1 – b3 – b2 – d3 – a4 (a4 – b2 – a1 – d3 – b3 – a4).
A:a1
B:d1
C:b4
D:b2
E:c2
pięciokąty ABCDE oraz ADBEC nie mają wspólnych boków.
Punkty: a1,d1,b2,c2,b4
5-katy: a1-b4-c2-b2-d1 i a1-b2-b4-d2-c2
5-katy mozna obracac i odbijac wiec w sumie rozwiazan bedzie osiem.
a
Przykładem dwóch takich pięciokątów są figury oparte na punktach : a1, c2, d2, b3, b4.
Boki pierwszej figury: a1-c2, c2-d2, d2-b3, b3-b4, b4-a1 ;
Boki drugiej figury: a1-d2, d2-b4, b4-c2, c2-b3, b3-a1 .