Ruchome lustro
Postanowiłem pochwalić się niedoróbką. Niby nie ma czym, ale ta wada ma pewną zaletę, a poza tym stanowi pretekst do zaprezentowania ciekawej łamigłówki. Pomysł nie jest mój. Ułożyłem po prostu zadanie oparte na cudzym pomyśle do zamieszczonego w listopadowym Świecie Nauki artykułu o labiryntach lustrzanych, a w zadaniu trafił się mały feler.
Mamy szachownicę 5 x 5, a właściwie kratownicę, bo czarno-biały deseń nie jest istotny. Na przekątnych niektórych pól stoją lustra, a na przekątnych wszystkich pozostałych pól – szyby. Z kilku miejsc przy brzegach planszy emitowane są na szachownicę – w wierszu lub kolumnie – promienie świetlne. Każdy „wędruje” jak wieża szachowa – odbijając się od niektórych luster – i opuszcza planszę. Przez szyby przechodzi bez zmiany kierunku (zakładamy, że szkło jest jak powietrze), więc nie ma znaczenia, na której przekątnej stoi szyba; na diagramie można ją zastąpić literą S. Odbijając się od lustra promień zostaje załamany, w tym przypadku pod kątem prostym, a więc ustawienie lustra jest istotne – może być mniej więcej takie „/” lub takie „\”.
W miejscu emisji znajduje się liczba oznaczająca, ile razy promień przechodzi przez szyby. Proszę zwrócić uwagę, że to nie to samo, co „przez ile szyb”, ponieważ na niektóre może trafić dwukrotnie.
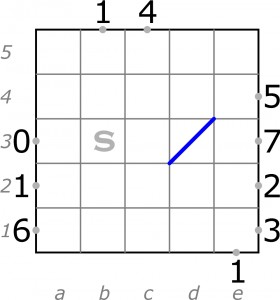
Oto przykład takiego lustrzanego labiryntu na planszy 4 x 4:
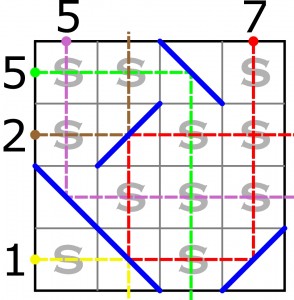
Zadanie polega na odtworzeniu układu luster na podstawie liczb. Dla ułatwienia zawartość dwóch pól jest ujawniona:
Prawdę mówiąc, ujawniłem jedno lustro i jedną szybę, żeby było jedno rozwiązanie. Tymczasem klops. Poniewczasie okazało się, że zadanie ma dwa rozwiązania, różniące się położeniem jednego lustra. Które dwa pola może zajmować to ruchome lustro? Krótka odpowiedź to zaleta niedoróbki, choć oczywiście można podać ustawienia wszystkich luster.
Poza rozwiązaniami mile widziane będą komentarze, dotyczące sposobu rozwiązywania. Głowy tęższe niż moja doszły do wniosku, że zadanie jest trudne oraz dominuje próbowanie i błądzenie, ale być może tęgie głowy Łamiblogowiczów odkryją jakąś wyraźną ścieżkę logiczną.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.

Komentarze
S/SS/
\SSSS
/SS/S
\SS/S
S//S\
Postaram się znaleźć to ruchome lustro…. 🙂
z mojego rozwiązania przesunąc lustro z B1 na C5 (bez obracania)
w sumie zadanie… nie było trudne… wręcz proste, mała plansza, mało możliwości. Lewy górny i prawy dolny róg rozwiązywało się od razu.
Znalezienie lustra… tez proste, bo jesli lustro (tylko jedno) trzeba przesunac, to wniosek nasunal sie taki ze musi ono byc na drodze tylko dwoch promieni, tych samych promieni. są takie dwa miejsca: B1 i C5, które tworzą drogę dla ‚6’ i ‚4’. Wystarczyło sprawdzić czy aby tylko w dobra strone promienie leca i wyjac lustro z jednego skrzyzowania i wsadzic w drugie, sprawdzić…. OK.
Może niejasno się wyraziłem: znalezc lustro na drodze dwóch promieni i sprawdzic czy te dwa promienie przecinaja sie na polu z szybą i te dwa pola wykorzsytac do sprawdzenia przestawienia lustra.
Hmmm, a może spróbować dla zmyłki zrobić takie zadanie, żeby w przypadku jednego promienia, ujawnione liczby zdradzały początek i koniec tego promienia, a trasę jednego zupelnie schować… 🙂 przełamałoby to tok rozumowania, że każda liczba musi wyjść na polu bez liczby 🙂
Ruchome lustro ‚/’ może zająć pola ‚b1’ lub ‚c5’.
Jedno z rozwiązań:
S / S S /
\ S S S S
/ S S / S
\ S S / S
S / / S \
Oprócz lustra na polu ‚a3’, trudno było mi znaleźć jakieś pewniaki.
Pomogło mi założenie, że promień wchodzący na planszę w miejscu oznaczonym liczbą (jest ich 10), opuści planszę w miejscu bez liczby (też 10). Mógłby wprawdzie pojawić się promień wychodzący z ‚1’ i wpadający do ‚1’, ale przyjąłem, że z powodu dużej odległości pomiędzy ‚jedynkami’, taka sytuacja nie wystąpi.
Założenia okazały się dobre i znalazłem rozwiązanie w około 10 minut.
Miałem przyjemność rozwiązywać zadania z listopadowego ŚN, a wśród nich i tego z aktualnego wpisu.
Jak sobie przypominam żadnego „mądrego” sposobu na zmierzenie się z tą łamigłówką nie miałem. Podczas rozwiązywania starałem się, aby promienie świetlne emitowane z najmniejszych liczb (0, 1, 2) miały jak najkrótsza długość, po to, aby mieć jak największe pole manewru przy wyznaczaniu promieni dla większych liczb.
Ogólnie, zadanie okazało się dla mnie bardziej zaskakujące (Dwa rozwiazania. A może więcej?), niż trudne.
Skoro już jesteśmy przy chwaleniu się, to i ja nie mam się czego wstydzić.
W zadaniu z rys.5 (ŚN – 11.2010) znalazłem nadmiar rozwiązań. A moja pomyłka wynikła z tego, że promień świetlny pomyliłem z kulą bilardową.
Najszybsza metoda to zauważenie, że skoro promienie muszą wyjść poza diagram (a jest ich 10) to muszą to zrobić w pozostałych 10 polach (ewentualnie 2 z 3 jedynek mogą się sparować, ale to powoduje postawienie dużej ilości luster), a potem to metoda prób i błędów w doborze wyjścia.
Skaczące lustro jest albo na polu b1, albo na polu c5.
Jeśli można zaproponować wpis na bloga, to chętnie poczytałbym coś na temat metazagadek, czyli zagadek o zagadkach, w których już zagadką jest treść zagadki 🙂
Dziękuję za podpowiedź. Będę powoli zmierzał do „mety-”
mp
W pierwszym przypadku mamy lustra :
/ a3,b5,b1,c1,d2,d3,e5
\ a4,a2,e1
w drugim przypadku mamy lustra:
/ a3,b5,c1,c5,d2,d3,e5
\ a4,a2,e1
Najpierw wyznaczyłam lustra dla 0, czyli a3,a4 (inaczej się nie da).
Następnie dla lewej 1, czyli a2 (inaczej się nie da)
Dalej dla dolnej 1, czyli e1,c1 (też jedyna możliwość)
Potem dla 2, czyli d2 (innej możliwości nie widzę)
Następnie dla 3, czyli e5 (dla mnie jedyna możliwość)
Potem sprawdzałam, czy gdy dla górnej 1 wezmę lustro b5 to rozwiążę to zadanie. Udało się.
Jeszcze dla górnej 1 można postawić dwa lustra: \b5 i / d5, ale dalej nie pasuje.
„Odbijając się od lustra promień zostaje załamany (…)”
Fizykom w tym miejscu podnosi się lekko ciśnienie 🙂 … ale na szczęście szybko opada dzięki skupieniu się na kolejnej ciekawej zagadce.
Gratuluję superciekawych, różnorodnych i wciągających łamigłówek z „Polityki”. Największe wrażenie zrobił na mnie wpis na pierwszej stronie, iż autorem tego pokaźnego zbioru jest jedna osoba – Pan. Chapeau bas!
Rzeczywiście, teraz i mnie ciśnienie skoczyło, ale już nie będę zacierał śladów swoich potknięć.
Dzięki za chapeau 🙂
m