Przegródki holenderskie
Po sudokowym przerywniku wrócę na moment do łamigłówek typu tatami, czyli polegających na dzieleniu pokratkowanego prostokątnego diagramu na prostokątne działki. Była już mowa o trzech rodzajach takich zadań, wszystkie mają japoński rodowód: shikaku, tatamibari oraz zwodnicze tatami. I na razie wystarczy. Pora zastąpić czworokątne maty różnymi wielokątami, czyli wejść na ścieżkę wiodącą do jednego z dań firmowych wydawnictwa Nikoli – łamigłówki fillomino.
W latach 80. Holendrzy jako pierwsi zaczęli publikować takie zadania pod nazwą „vakken vullen”, czyli wypełnianie przegródek (określenie to ma w języku niderlandzkim także inne – handlowe znaczenie).
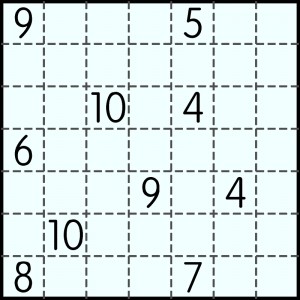
Zaczniemy od prostych przegródkek:
Diagram należy podzielić wzdłuż przerywanych linii na wielokąty różnej wielkości. Każda liczba oznacza, z ilu kratek składa się wielokąt, którego częścią jest kratka z tą liczbą.
W praktyce rozwiązywanie polega na wypełnianiu kratek liczbami (stąd nazwa zadania) tak, by w efekcie końcowym w każdej kratce należącej do wieloboku złożonego z x pól znalazła się liczba x.
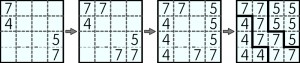
Oto dziecinnie prosty przykład, ilustrujący tok rozwiązywania:
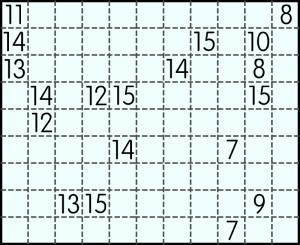
I drugi, nieco większy, ale czy twardszy orzech?:
W rozwiązaniu każdego zadania wystarczy podać, z ilu kratek składają się występujące w podziale dziesięcioboki.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.

Komentarze
Zad. 1. Dwa dziesięcioboki: 8 i 9
Zad. 2. Jeden dziesięciobok: 8
Moim zdaniem trudne. Ciężko znaleźć punkt zaczepienia.
9+8, 8 jeśli dobrze liczę.
W pierwszym diagramie dziesięciobokami są wielokąty złożone z 8 i 9 kratek, a w drugim z 8 kratek.
Ponieważ po podziale wielokąty muszą być różnej wielkości, to wszystkie jednakowe liczby muszą należeć do jednego wielokąta. W związku z tym istota rozwiązania sprowadza się do utworzenia wielokąta z „czternastkami” i wielokąta z „piętnastkami”. Reszta już nie stanowi żadnego problemu.
http://pokazywarka.pl/f4ziw9-2/
Jak widać istnieje jeden dziesięciobok składający się z ośmiu kratek.
Pozdrawiam,
jazz
1) dwa 10-boki – 8- i 9-polowy.
2) 10-bok 8-polowy.
Zadanie 2 wyraznie latwiejsze – wieksze wielokaty, wiecej informacji, mniej mozliwosci kombinowania.
a
No tak, zapomniałem o pierwszym zadaniu. Tu mamy dwa dziesięcioboki: ośmio- i dziewięciokratkowy.
Te tak zwane proste przygródki zajęły mi więcej czasu od tego ‚twardego orzecha’. Nie wiem dlaczego, być może dlatego, że jest conajmniej 7 rozwiązań (tyle znalazłem) ‚łatwiejszego’ zadania.
Oj, wycofuję się!!! to łatwiejsze zadanie źle przerysowałem 🙂 🙂 🙂 No… ale rozwiązałem i… to się liczy 🙂
1. Mamy tu 2 dziesięcioboki składające się z 8 i 9 kratek.
2. Jeden dziesięciobok z 8 kratek.
Dla mnie oba problemy powyżej średniego poziomu trudności. Czasy rozwiązania:15 i 17 minut.
http://pokazywarka.pl/d5zg0d-2/
Zastanowienie nad 14-tką i 15-tką prowadzi do jednego możliwego układu 12-tki. A potem okazuje się, że 14-tka z 15-tką mają ujawnione pola krańcowe i dalej już idzie łatwo.