Parasol
Na zamówienie pewnego dziennika ułożyłem trzy sudoku obrazkowe. Kiedyś nazywałem tę odmianę graffiti, ale doszedłem do wniosku, że określenie jest zbyt ekstrawaganckie, a niezbyt adekwatne. Przypomnę, że chodzi o zwykłe, „staroświeckie” sudoku, wyróżniające się tylko formalnie tym, że początkowy układ cyfr tworzy jakiś symboliczny rysunek. Odmiana jest modna od mniej więcej roku w kręgach zbliżonych do Thomasa Snydera.
Zamawiający dziełka narzekają niekiedy na „toporność” obrazka. Tłumaczę, że na kwadracie 9×9, a więc dysponując 81 pikselami, esów-floresów przedstawić się nie da; nawet linie ukośne są wyraźnymi schodami.
Mam zwyczaj po ułożeniu i sprawdzeniu, że rozwiązanie jest jedno, odkładać zadanie na dzień lub dwa do szuflady, żeby dojrzało. Potem wyjmuję je i rozwiązuję na luzie, sprawdzając stopień trudności, a na koniec zazwyczaj przesyłam komuś ze znajomych łamigłówkarzy z prośbą o opinię i potwierdzenie moich czasów.
W przypadku trzech wspomnianych zadań rozwiązywanie pierwszego zajęło mi mniej więcej 10 minut, a każdego następnego o 5 minut więcej. Poprosiłem Janka Mrozowskiego, aby swoimi rezultatami potwierdził moje. No i potwierdził: jedno sudoku zajęło mistrzowi 104, drugie 108, a trzecie 116… sekund. Chyba źle wybrałem testującego…
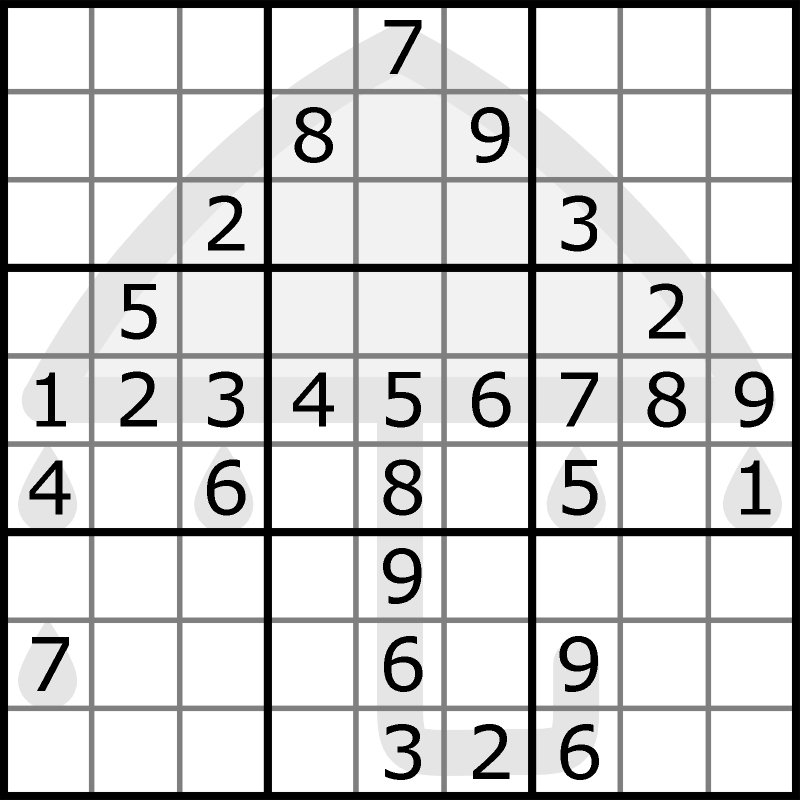
Od niedawna nasz as łamigłówkowania, a zwłaszcza sudokowania, bloguje – i to w dwóch językach: po polsku i po angielsku. Na blogach pojawiają się ciekawe, oryginalne zadania autorskie. Prywatnie ostatnio sporo dyskutuję z Jankiem na temat różnych pomysłów i trendów w łamigłówkowym światku, np. o tzw. strzelaniu, czyli próbowaniu i błądzeniu w trakcie rozwiązywania. Zapewne wkrótce więcej popiszę na ten temat w Łamiblogu. A tymczasem, pozostając przy sudoku obrazkowym (ale też nie całkiem odbiegając od strzelania), propozycja na zbliżające się wiosenne, ale deszczowe dni.
Gdyby ktoś z Państwa chciał się pochwalić rozwiązaniem, to wystarczy podać cztery cyfry, które znajdą się w rogach diagramu. Mile widziane będą także informacje o czasie rozwiązywania.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3 dni.

Komentarze
Nienawidzę sudoku. Jest to jedna z niewielu łamigłówek, których staram się unikać. Czasem jak trafię na jakieś, to na przekór sobie rozwiązuję. Na widok „Parasolki” też pomyślałem: „A, rozwiążę sobie” Eh… Przez 15 minut jakoś to szło, ale w ciągu ostatnich 15 minut nie wpisałem ani 1 cyfry :/ .
Pozdrawiam
Michał
Czy toto sie da w ogole rozwiazac do konca na logike. Bo moim zdaniem nie.
A przeciez podanych jest az 28 cyfr, to sporo jak na zwykle sudoku.
a
Wpisy Michała i andy’ego na tyle mnie zafrapowały, że pokuszę się o rozwiązanie tego sudoku, mimo iż podzielam niechęć Michała (może nie aż tak bardzo) do sudoku.
6,5,5,7
Po wpisaniu 27 cyfr strzelałam w pierwszej kolumnie 5i9. najpierw nie trafiłam, potem rozwiązywało się bez zgadywania. Niestety 19min
Też uważam, że musi być jeden strzał. To zresztą wynika z wpisu
” A tymczasem, pozostając przy sudoku obrazkowym (ale też nie całkiem odbiegając od strzelania)”. Rozwiązanie sudoku:
6 4 8 3 7 1 2 9 5
3 7 5 8 2 9 1 6 4
9 1 2 6 4 5 3 7 8
8 5 7 9 1 3 4 2 6
1 2 3 4 5 6 7 8 9
4 9 6 2 8 7 5 3 1
2 6 1 7 9 4 8 5 3
7 3 4 5 6 8 9 1 2
5 8 9 1 3 2 6 4 7
Zajęło mi to około 20 minut.
Pozdrowienia
Na logikę moim zdaniem da się wpisać 28 następnych cyfr. Żeby wpisać pozostałe 25 trzeba stosować metodę prób i błędów.
Oczywiście z tych 28 początkowych cyfr nie wszystkie sa potrzebne. Można na przykład ze środkowego wiersza usunąć cyfry 2, 5 i 8, bo ich położenie można od razu jednoznacznie określić. Ale ciekawa jest sprawa z „kropelką” w lewym dolnym kwadracie. Usunięcie cyfry 7 powoduje, że zadanie zamiast jednego ma 803 rozwiązania.
Podniosły mnie na duchu pierwsze wpisy o konieczności zgadywania…
(….) BEZ ZGADYWANIA (??? mp), ale z czasu nie mogę być zadowolony (? mp) 7:35 (! mp 🙂 )
pozdr
Hm, nie mam sił się przyglądać, czy się nie pomyliłem w moim rozumowaniu i czy w takim razie nie był to po prostu strzał. W każdym razie w r9k3 wykluczyłem na podstawie założenia o jednym rozwiązaniu diagramu zarówno 1 4 5 7. 8 szybko jakoś się wykluczała również i pozostała 9. Teraz tego nie widzę za bardzo, a ciężko mi się wchodzi do tej samej rzeki dwa razy 🙂
7 tam być nie mogła, bo jest już od początku w r8k1. 1, 4 i 5 – zgoda, bo w 3 kolumnie 8 i 9 mogą być tylko w 1 i 9 wierszu. Jednak 8 chyba tak szybko nie da się wyeliminować. Ale nawet przyjęcie, że w r9k3 musi być 9 wcale nie prowadzi natychmiast do końca, bo rozstrzyga tylko położenie cyfr w lewym dolnym kwadracie i częściowo w lewym górnym.
w rogach znajdują się cyfry 6 5 5 i 7.
rzeczywiście pierwsze 28 cyfr znajdowało się dosyć szybko, ale potem nie udało mi się rozwiązać bez zrobienia jednego założenia. Ciężko mi więc mówić o czasie rozwiązania. 😉
Nie liczyłem czasu rozwiązania bo wyszedłby za długi:) tym bardziej, że rozwiązywałem z 5 razy z doskoku (ale się przykładałem!) i niestety bez zgadywania sie nie obyło. Po wpisaniu 27 czy tez owych 28 liczb, musiałem zgadywać, zwykle (a doświadczenia wielkiego nie mam) tak zwane zgadywanie polega na tym, że po trzeciej lub czwartej liczbie widać, że ruch był zły, w tym zadaniu nie za bardzo. Specjalnie poszedłem złym tropem i znowu doszedłem do sytuacji, w której musiałbym zgadywać.
Oto moje pierwsze rozwidlenie dróg:
6__37_2__
3__82916_
__264_3__
857913426
123456789
496287531
26__948_3
73__689_2
____326__
po ‚zgadnięciu’ r3-k8 liczby ‚7’ wszystko poszlo jak z płatka.
6
Też ostatnich 25 cyfr nie udaje mi się wydedukować. A jak jest strzelanie to ja się zniechęcam, bo to przestaje być łamigłówka.
Z wykluczeniem 8 w r9k3 nie ma aż tak dużego wysiłku.
8 r9k3, czyli 9 w r1k3 czyli 5 w r3k1 czyli 5 w r1k6 czyli druga 9 w rzędzie 1 w kolumnie 8 (tu może być tylko 59 – 4 jest wykluczone, gdyż gdyby nie było 4 w kolumnie 8 w rzędach 89 to mielibyśmy 157 w kolumnie 8 w ostatnim sektorze i 157 w kolumnie 4 w przedostatnim sektorze, co w danej sytuacji dałoby nie jedno rozwiązanie zadania – zatem w r1k8 jest 59 a w r9k9 57 z powodu tej 4).
A po wpisaniu 9 w r9k3 idzie do końća jak po sznurku. Nie widzę problemów
Nie podoba mi się metoda, polegająca na przyjmowaniu założenia, że „zadanie musi mieć dokładnie jedno rozwiązanie” i wykluczanie na tej podstawie pewnych układów liczb. Może nie tyle sama metoda, co zadanie, które da się rozwiązać „logicznie” tylko taką metodą. Zresztą w tym zadaniu droga od wstawienia cyfry 8 w r9k3 do wykorzystania tego założenia jest na tyle długa, że można uważać takie rozwiązanie, za oparte na metodzie prób i błędów.
Po wpisaniu 9 r9k3 rzeczywiście wszystko da się logicznie wywnioskować.
pafcio: jesli rozumiem dobrze zapis r1k3, ze to rzad pierwszy kolumna 3 licza od gornego lewego rogu, to jakos nie zgadza mi sie z rozwiazaniem. We wpisie poprzednim przytoczylem czesc rozwiazania do momentu gdzie musialem zgadywac, ale czytajac post zmuszony jestem podac cale rozwiazanie by moc je potem skonfrontowac (zostawiajac je na kartce, pozbawilbym sie jego na dobre i musial jeszcze raz rozwiazywac:) )
648371295
375829164
912645378
857913426
123456789
496287531
261794853
734568912
589132647
🙂 czytam bez zrozumienia 🙂 przeczytalem jeszcze raz i zrozumialem wywód pafcia 🙂
Do pafcio: „Z wykluczeniem 8 w r9k3 nie ma aż tak dużego wysiłku.”
Niby jak, bo ja nic logicznego nie mogę wymyślić:/