Trochę mięska
Dział matematyki rekreacyjnej, obejmujący zadania, które polegają na odtwarzaniu pełnego zapisu działania arytmetycznego na podstawie jego „szczątków”, zwany jest arytmetyką szkieletową. Nazwa kojarzy się ze stosowaną m. in. w archeologii i kryminalistyce rekonstrukcją antropologiczną wyglądu twarzy na podstawie zachowanej czaszki. W działaniu arytmetycznym, którym zwykle jest mnożenie lub dzielenie, szkielet tworzą miejsca po cyfrach (i na cyfry), czyli puste kratki.
Antropolog dysponuje gołą czaszką i metodą Gierasimowa. Główkołamacz z całkowitą „golizną” ma bardzo rzadko do czynienia. Nie ruszy z miejsca, jeśli nie dostanie trochę „mięska”, czyli dodatkowej informacji w postaci choćby jednej ujawnionej cyfry lub podpowiedzi w rodzaju: w zapisie nie występuje zero albo…
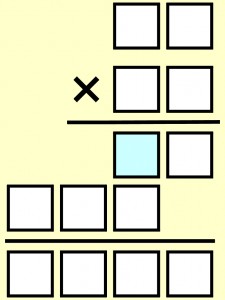
…wszystkie cyfry są nieparzyste, oprócz jednej – w niebieskiej kratce.
Ogólna nazwa takiej łamigłówki bywa różna. W języku angielskim obok szkieletowego mnożenia lub dzielenia zadanie często występuje jako kryptarytm (np. w artykułach Martina Gardnera), co w tym przypadku nie jest ścisłe, bo „szyfru” brak. W Polsce i w wielu innych krajach zaliczane bywa do tzw. rebusów matematycznych lub liczbowych, co również jest raczej umowne niż sensowne. Przed -dziestu laty często gościło na łamach jako zamazane lub zaplamione działanie. Pod nazwą, której geneza jest podobna – molowe rachunki – znane jest w Chinach i Japonii, gdzie jako gimnastyka szarych komórek cieszyło się dużym wzięciem już w XVIII wieku. Nietrudno zgadnąć, skąd określenie molowe: działanie zapisano na papierze, a papier powygryzały mole.
Dwa zadania należące do arytmetyki szkieletowej uchodzą za klasyczne i wzorowe. Przede wszystkim ze względu na minimalną liczbę ujawnionych cyfr, czyli jedną oraz odpowiedni ciężar gatunkowy i oczywiście jedno rozwiązanie. Pierwsze to samotna siódemka opublikowana w roku 1922 na łamach brytyjskiego miesięcznika Strand Magazine. Drugie – samotna ósemka z American Mathematical Monthly z roku 1954.
Idealna i wciąż krzepka, choć już niemłoda para – poniżej w całej okazałości.
Czy komuś z Państwa uda się zmóc oba zadania? No, nie wiem… Na sam widok można się poddać, chociaż… pozory mogą mylić.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3 dni.


Komentarze
W obu przypadkach dzielnikiem jest 124, a błękitna to 4.
Pozdrawiam PM.
15 x 93 = 45 + 135 = 1395
Co do ostatnich to ja się jak najbardziej poddaję na sam widok.
😉 ? mp
Jedna parzysta
15 x 93 = 1395
Rozwiązanie zadania z jedną 8 najłatwiej jest „znaleźć” w książce L. Pijanowskiego „Rozkosze łamania głowy” na stronie 104. Dla porządku je przepiszę 10020316:124=80809. Podany jest tam też sposób rozwiązania. Zamiast 8 można w tym zadaniu wstawić 7 i nowe zadanie też ma jedno rozwiązanie.
A zadanie z jedną siódemką rozwiązuje się tak samo jak to z jedną ósemką. 12128316:124=97809
Hmmm. Pierwsze zajęło mi więcej czasu niż pozostałe razem wzięte:
(no i nie musiałem użyć bezczelnie faktu, że dzielnik jest ten sam)
93*15 = 45+135 = 1395
10020316 : 124 = 80809
12128316 : 124 = 97809
Z rozwiązaniem „samotnej siódemki” nie miałem żadnych problemów. Myślałem, że i z „samotną ósemką” poradzę sobie bezproblemowo, bo istnieje między tymi zadaniami pewne podobieństwo, ale nie dałem rady znaleźć rozwiązania.
Czy za „samotną ósemką” nie kryje się jakiś podstęp? Jeśli tak nie jest, to chyba pod wpływem trzaskającego mrozu zapadłem w zimowy letarg.
Ach, włączę się do zabawy. Jak zwykle pomaga bezgraniczne zaufanie do autorów zadania, że skoro dali zadanie to _musi_ mieć rozwiązanie. I to jedno 🙂
15*93
12128316:124
oraz 10020316:124
Ale to i tak pikuś w porównaniu do polewania wodą, siedzę nad nim do tej pory i ciągle mi się wymyka…
1)15×93=1395
2)97809×124=12128316
3)Jedynie 80809×124=10020316 pasuje w tym mnożeniu. Może w tym wypadku samotna znaczy- na podstawie jednej cyfry odtwórz mnożenie?
Po rozwiązaniach widzę, że tylko mi przyszedł do głowy pomysł, że „samotna siódemka” i „samotna ósemka” oznacza w obu przypadkach – jedna cyfra w działaniu. Nie dziwię się zatem, że nie dałem rady „samotnej ósemce”, bo przy takim założeniu była ona nie do rozwiązania.