Wśród drzew

6 stycznia 2010
Marek Penszko

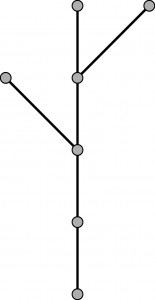
Oto drzewo, nie wyglądające zbyt okazale.

Przypomina resztki szkieletu choinki albo pewien gatunek kaktusa, którego nazwy nie pamiętam.
W teorii grafów taki badyl, złożony z wierzchołków (punkty) i łączących je krawędzi (odcinki) nazywa się właśnie drzewem. Aby jednak zasługiwał na to określenie, każde dwa wierzchołki powinna łączyć jedna i tylko jedna droga. Ponadto, by drzewo przypominało drzewo, zwykle wyróżnia się w nim jeden wierzchołek, zwany korzeniem, a pozostałe rozmieszcza tak, aby wraz z łączącymi je krawędziami tworzyły jakby koronę, choć na ogół niezbyt bujną.

Drzewo na rysunku ma 7 wierzchołków oraz średnicę, która wynosi 4. Średnica drzewa-grafu to najdłuższa – złożona z największej liczby odcinków – droga między dwoma wierzchołkami; jednostką długości jest więc krawędź, czyli w tym przypadku kot wspinający się na drzewo „zaliczy” co najwyżej 4 krawędzie. Ze złażeniem na dół koty miewają zwykle kłopoty, więc cofanie się wykluczamy.
Czy istnieją inne drzewa o 7 wierzchołkach i średnicy równej 4?
Owszem, jeszcze cztery. Oto one:

W sumie zatem wszystkich drzew z 7 wierzchołkami i średnicą równą 4 jest 5.
Mam nadzieję, że teraz będzie zrozumiałe stwierdzenie, dotyczące osobliwego związku liczby 2010 z teorią grafów:
Różnych  drzew z 15 wierzchołkami, których średnica wynosi 7 jest dokładnie 2010.
Poniższa łamigłówka jest także „drzewna”, ale wiąże się z zupełnie innymi działami dendrologii i matematyki.

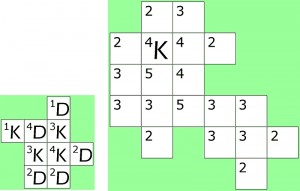
W każdym polu należy zasadzić drzewo (D) lub krzew (K).
Cyfra w polu z D powinna oznaczać liczbę sąsiadujących z tym polem kratek z K.
Cyfra w polu z K powinna oznaczać liczbę sąsiadujących z tym polem kratek z D.
Sąsiedztwo to stykanie się bokiem lub rogiem.
Dla jasności – mały przykład z lewej.

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3 dni.