Indugadka
Dawno nie prezentowałem łamigłówek indukcyjnych. Przeglądając dotychczasowe zauważyłem, że wszystkie indugadki – jak nazwał je Bazyli w komentarzu ponad pół roku temu – należą do tej samej rodziny, którą można by nazwać kwadratami liczbowymi. Polegają na wpisywaniu liczb w diagram n x n, czyli są mniej lub bardziej spokrewnione z kwadratami łacińskimi.
Wprost trudno uwierzyć, ile różnych sposobów łamania głowy wyciśnięto z poczciwych kwadratów łacińskich od czasu sudokowej epidemii. Nawet nie modyfikując podstawowej reguły (w każdym rzędzie i w każdej kolumnie powinny znaleźć się cyfry od 1 do n) japońscy autorzy wyprodukowali jak dotąd blisko setkę różnych rodzajów zadań. Większość z nich nie wychynęła poza pisma specjalistyczne, bo są zbyt wyszukane, aby mogły liczyć na większe zainteresowanie. Na szersze wody, zwłaszcza te internetowe, wypływają nieliczne. Od półtora roku Anglicy i Amerykanie lansują KenKen, ze skutkiem takim sobie. Jest to jednak zabawa, która się zapewne ostanie, bo ma dodatkowe walory edukacyjne – nie tylko wymaga logicznego myślenia, jest także ćwiczeniem poprawiającym sprawność rachunkową.
Wracając do indugadek, przypominam, że są one typu „dwa w jednym”. Zadanie nie ma opisu, czyli na początku nie wiadomo, jak się do niego zabrać. Zamiast tego podany jest mały przykład z rozwiązaniem i na tej podstawie trzeba samemu rozszyfrować, o co w tym wszystkim chodzi. A gdy już będzie wiadomo, co jest grane, można zabrać się za właściwą łamigłówkę.
Oto przykład:
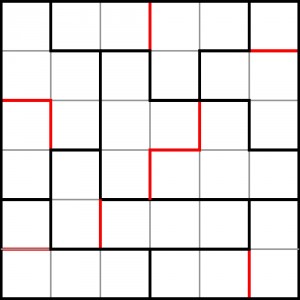
I łamigłówka do rozgryzienia po rozgryzieniu reguł zabawy:
Uprzedzam lojalnie, że oba etapy są… nietrudne, takie dla początkujących „induktorów”. Twardy (nawet bardzo) orzech indukcyjny pojawi się w następnym wpisie. Pora ostrzyc zęby.
PS Autora dziesiątego nadesłanego rozwiązania w konkursie z wpisu „Drugi mecz” proszę o wybór drobnego upominku (gry „6 bierze!” lub książki „Łamigłówki. Podróże w krainę matematyki rekreacyjnej”) oraz o podanie adresu, pod który nagroda ma być wysłana. Informacje te proszę przesłać jako komentarz do niniejszego wpisu (nie będą ujawnione). The winner is… bloodlord!
PS 2 Przepraszam za byczka, w prawym górnym rogu przykładu. Po Państwa uwagach poprawiłem się z piątki na pałę.


Komentarze
najbardziej mnie zaskakuje i martwi „piątka” w przykładzie… gdyby tam była jedynka, to wszystko by się zgadzało… a tak, to nie wiem
Hmmm. Gdyby zamiast 5 byla 1, to zasada bylaby b. prosta:
1) w wierszach i kolumnach rozne liczby
2) W kazdym obszarze wyznaczonym czarna linia, czerwona linia dzieli sume na dwie polowy.
Ale jest 5, co moze dawac takie zasady:
1) j.w.
2) wykonujac pewne dzialanie (+ lub -) na liczbach w obu czesciach czarnego obszaru musi wyjsc ten sam wynik i oba dzialania musza sie pojawic?
Jakby zamiast ‚5’ było ‚1’ to wszystko by mi pasowało, łącznie z regułą obowiązującą w tym zadaniu. Chciałbym tylko się upewnić, że tam na pewno jest ‚5’ a nie ‚1’.
Zakładając, że w miejscu piątki powinna być jedynka, pasuje rozwiązanie:
164235
346521
415362
523614
652143
231456
164235
346521
415362
523614
652143
231456
164235
346521
415362
523614
652143
231456
164235
346521
415362
523614
652143
231456
Czerowna kreska oddziela równe sobie sumy w czarnych figurach.
164235
346521
415362
523614
652143
231456
Witam
Faktycznie nietrudne.
164235
346521
415362
523614
652143
231456
Pozdrawiam
164235
346521
415362
523614
652143
231456
1 6 4 2 3 5
3 4 6 5 2 1
4 1 5 3 6 2
5 2 3 6 1 4
6 5 2 1 4 3
2 3 1 4 5 6
Rzeczywiscie, miekki orzeszek:
1 6 4 2 3 5
3 4 6 5 2 1
4 1 5 3 6 2
5 2 3 6 1 4
6 5 2 1 4 3
2 3 1 4 5 6
a