Drugi mecz

7 lipca 2009
Marek Penszko

Czy układanie, wymyślanie, projektowanie łamigłówek jest sztuką? Jeśli rozumianą jako „kunszt, mistrzostwo”, to na pewno może tak być i bywa. Wytwory tej sztuki mogą także dostarczać wrażeń estetycznych, podobnie jak piękne mogą być dowody matematyczne. Zdarza się, że teoretycy „sztuki łamigłówkowej” górnolotnie przyrównują ją do niektórych sztuk pięknych. Wydaje się to jednak lekką przesadą, bardziej adekwatne byłoby zestawienie ze sztuką kulinarną – takie określenie pichcenia pasuje do wyczynów mistrza patelni, ale gdy smażę jajecznicę, to raczej sztuki nie uprawiam. Podobnie nie każdy autor łamigłówek jest „sztukmistrzem”. W obu dziedzinach jest mniej więcej tyle samo miejsca na oryginalną twórczość, a rozkosze podniebienia można przyrównać do rozkoszy łamania głowy. I podobnie jak smakosz z żyłką do kucharzenia prosi o przepis, by samemu spróbować zrobić jakiś cymes, tak łamacza głowy z twórczym zacięciem kusi, aby zmierzyć się z ciekawym pomysłem zaproponowanym przez innego autora. Dlatego spróbowałem ułożyć piłkarskie sudoku na wzór dziełka Jana Novotnego zaprezentowanego we wpisie Futboldoku.

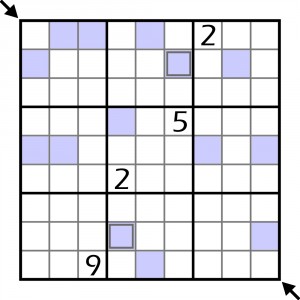
Prawie wszystkie szczegóły i zasady rozwiązywania są takie same, jak w zadaniu z poprzedniego wpisu. Proszę więc przed rozwiązywaniem do tego wpisu zajrzeć i dokładnie przeczytać tekst, korzystając także z przykładowego diagramu ilustrującego zasadę podawania piłki. Poniższe zadanie różni się tylko jednym szczegółem: dozwolone są loby, czyli piłka może przelecieć w trakcie podania „przez” zawodnika przeciwnej drużyny, ale wszyscy (dwaj) przelobowani gracze wskazani są na diagramie – znajdują się w polach z kwadratami.

Zadanie jest konkursowe. Termin nadsyłania rozwiązań, jako komentarzy do tego wpisu – 5 dób (tym razem dłużej, bo to nieco twardszy orzech) od pojawienia się wpisu. Komentarze z rozwiązaniami nie będą ujawniane przed upływem podanego terminu. Nagrodę (gra 6. bierze! lub książka Łamigłówki. Podróże w krainę matematyki rekreacyjnej – do wyboru) otrzyma osoba, która nadeśle N-te rozwiązanie. N jest dzielnikiem sumy liczb (S) na przekątnej wskazanej strzałkami, który okaże się najbliższy liczbie nadesłanych rozwiązań, ale oczywiście nie większym od niej. Jako rozwiązanie wystarczy podać S.