Okresowo i nie
Tak sobie myślę, czy nie byłoby sensownie zastąpić Dzień Pierwiastka Kwadratowego, o którym wspominałem w poprzednim wpisie, Dniem Pierwiastka w ogóle, a więc bez podawania stopnia. Okazji do świętowania byłoby wówczas nieco więcej, czyli w ciągu wieku tuzin, a wszak to liczba o długiej tradycji, podstawa rozpowszechnionego niegdyś dwunastkowego systemu liczbowego, do dziś zresztą stosowanego w rachubie czasu. Nie zamierzam oczywiście robić konkurencji panu Gordonowi, ale nie omieszkam mu przy okazji zasugerować.
Tymczasem postanowiłem postać jeszcze chwilę na drugim stopniu schodków. Określenie „schodki” jest o tyle uzasadnione, że kojarzy się z cokolwiek rozrywkowym sposobem zapisu pierwiastków kwadratowych (z liczb całkowitych, które nie są kwadratami), odkrytym przez Lagrange’a przed 230 laty. Ściślej chodzi o zapis ich części ułamkowej w postaci nieskończonego ułamka łańcuchowego. Dla sqrt2 wygląda to tak:
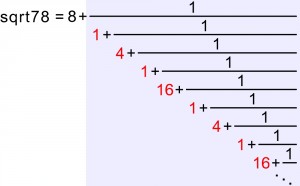
Więcej odwróconych różnych schodków pojawia się np. dla sqrt78:
Najciekawsze jest to, że ciąg czerwonych liczb jest zawsze okresowy. Dla sqrt2 okres jest jednoelementowy, czyli ciąg jest stały, a dla sqrt78 składa się z czterech liczb [1,4,1,16,….]. Bywają jednak znacznie dłuższe okresy, na przykład 102-cyfrowy dla sqrt2566.
Dla odmiany w przypadku innych zagadnień związanych z pierwiastkami kwadratowymi zaskoczeniem może być – przynajmniej w pierwszej chwili – brak okresowości.
Z okazji Dnia Pierwiastka Kwadratowego chłopiec otrzymał skarbonkę i postanowił zasilać ją codziennie kwotą sqrt2 euro. Ponieważ o taką kwotę niełatwo, więc zdecydował, że będzie wrzucał każdego n-tego dnia an euro – a konkretnie taką monetę, aby suma zebrana w ciągu n kolejnych dni, poczynając od n=1, była jak najbliższa wartości n*sqrt2. W skarbonce pojawiały się więc wyłącznie monety o wartości 1 i 2 euro. Zaczęło się od a1=1, a dalej było: a2=2, a3=1, a4=2, a5=1….
Proszę udowodnić, że ciąg wartości kolejno wrzucanych monet będzie – wbrew pozorom – nieokresowy.
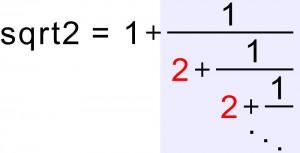

Komentarze
Wszystkim komentującym w Łamiblogu Paniom, Dziewczynom i Kobietom moc serdeczności z okazji Ich Dnia przekazuje
Jazz
Ładne rozwiniecie w ulamek lancuchowy ma tez liczba „e”:
2;121 141 161 181 … (kolejne cyfry to kolejne „czerwone liczby”)
Jeśli ciąg wartości monet wrzucanych do skarbonki miałby być okresowy np. o okresie M-elementowym, a suma zebrana w ciągu kolejnych M dni byłaby równa S euro, to średnio każdego dnia do skarbonki trafiałaby, wyrażona w postaci liczby wymiernej, kwota S/M euro. Natomiast sqrt(2) jest liczbą niewymierną, co wykazuje błędność założenia okresowości ciągu.
Ufff. Zdazylem przed uwolnieniem rozwiazan. Moje moze byc przekombinowane, ale potrzebowalem „modelu” tego co sie dzieje w zadaniu.
a) Zamiast sqrt(2) bede rozpatrywal sqrt(2) – 1. (czyli od kazdego elementu ciagu odejmuje 1)
b) Wyobrazmy sobie okrag dlugosci jeden z wyróżnionym punktem poczatkowym (powiedzmy punktem skrajnie prawym) -> oznaczmy go przez P.
c) Na okregu zaznaczamy dwie polowki (gorna i dolna; albo jak kto woli przed P i za P.
I. Zaczynamy w P i przesuwamy sie na okregu o sqrt(2)-1 w kolejnych krokach.
II. Jesli ladujemy w dolnej polowce to piszemy 0, jesli w gornej, to 1.
III. Ciag, ktory wypisalismy, to ciag a_n (pomniejszony o jeden).
1. Zalozmy teraz, ze nasz ciag jest okresu N -> tzn. a_1=a_{N+1}.
2. Popatrzmy na obrot o N*(sqrt(2)-1), czyli na podciag a_{kN+1} dla kolejnych k=0,1,2…
3. Ciag a_n byl okresowy, czyli nowy ciag jest staly; ale tez pochodzi od obrotu o kąt niewymierny -> a to jest niemozliwe. (obrot nie moze byc o zero stopni ani o 180; zatem bedzie mniejszy niz 180, czyli w drugim kroku trafimy w gorna polowke)
Ad.3. jesli liczymy miare w stopniach powinienem napisac zamiast „niewymierny” – „niewspolmierny z Pi”.
Zapomnialem -> oczywiscie tak samo mozna pokazac, ze ciag nie jest okresowy od pewnego miejsca. (czyli ze a_p=a_(N+p) dla p wiekszych od jakiejs liczby).