Dowodzę
We wpisie z 19 marca zamieściłem poniższe zadanie.
Na wielościanie wypukłym jest tyle mrówek, co ścian. Każda ściana należy do jednej mrówki i każda z nich cały czas wędruje po krawędzi wokół swojej ściany zgodnie z ruchem wskazówek zegara. W ciągu godziny każda mrówka przemieszcza się co najmniej o 1 milimetr. Należy dowieść, że po pewnym czasie jakieś dwie mrówki na pewno się spotkają.
Prawdę mówiąc, nie przypuszczałem, że ktoś spróbuje rozgryźć ten orzech, zamieszczony właściwie tylko na poparcie stwierdzenia, że mrówcze problemy mogą być bardzo trudne (zadanie pochodzi z eliminacji do rosyjskiej olimpiady matematycznej sprzed kilkunastu lat). Nie doceniłem więc osób, które podjęły wyzwanie, tym samym wywołując mnie do tablicy.
Nie podejmuję się, przynajmniej na razie, oceniać dowodów lub szkiców dowodów zamieszczonych w komentarzach, między innymi dlatego, że niektóre fragmenty są dla mnie niejasne. Bardzo możliwe, że podany przez Andrzeja69 dowód jest poprawny, choć różni się od znanego mi; jak wiadomo, to samo twierdzenie można rozgryzać na wiele sposobów, na przykład prawo wzajemności reszt kwadratowych ma grubo ponad 150 różnych dowodów.
Zgodnie z zapowiedzią, poniżej wystawiam na krytykę ów dowód „oficjalny”. Starałem się, by opis był zwięzły, więc nie wykluczam, że niektóre jego fragmenty mogą wydać się „śliskie”, czyli wymagające dodatkowych wyjaśnień.
Dowód
1. Zakładamy, że do spotkania nie dochodzi, czyli mrówki obchodzące sąsiednie ściany nie mogą znaleźć się równocześnie na wspólnej krawędzi, bo wówczas musiałyby się na tej krawędzi spotkać.
2. Nazwiemy pozycją rozmieszczenie wszystkich mrówek na konkretnych krawędziach, a ruchem, prowadzącym do powstania nowej pozycji – przejście jakiejś mrówki na następną krawędź.
Liczba pozycji jest skończona, więc będą się one powtarzać, zatem ciąg ruchów bez spotkań można uznać za cykliczny. Inaczej mówiąc: wychodząc od jakiejś pozycji można powrócić do niej po zaliczeniu pewnej liczby innych pozycji.
3. Rysujemy na powierzchni wielościanu mapę: na każdej ścianie-kraju oznaczamy niebieski punkt-stolicę i każdą parę stolic sąsiednich ścian łączymy drogą (zielona) przecinającą wspólną krawędź (czarna). Na skrzyżowaniach krawędzi z drogami umieszczamy mrówki (brązowe groty), tworząc tym samym konkretną pozycję. Każda mrówka jest przesunięta na swoją ścianę; grot wskazuje zegarowy kierunek jej ruchu.
4. Dodatkowo pozycję oznaczamy trasując wszystkie drogi przecinające krawędzie z mrówkami, czyli zaczerwieniamy je i stawiamy strzałki określające ich kierunek – zawsze z prawa na lewo z punktu widzenia idącej mrówki.
5. Z każdej stolicy wychodzi dokładnie jedna trasowana droga wiodąca do sąsiedniej stolicy, zatem niektóre z tych dróg będą w każdej pozycji tworzyć obwodnice – jednokierunkowe trasy okrężne.
Każda obwodnica dzieli powierzchnię wielościanu na dwie części. Tę, którą obwodnica okrąża w kierunku zgodnym z ruchem wskazówek zegara, nazwiemy częścią wewnętrzną – do niej kierują się wszystkie znajdujące się na obwodnicy mrówki-groty, które mogą wykonać ruch.
6. Wybieramy obwodnicę, wewnątrz której nie ma innej obwodnicy (w następstwie ruchów w jej wnętrzu może pojawić się nowa obwodnica, wówczas na nią się przeniesiemy) – oznaczona czerwoną przerywaną linią.
Obwodnica zmienia kształt i „zacieśnia się” po każdym możliwym do wykonania (nie prowadzącym do spotkania) ruchu dowolnej znajdującej się na niej mrówki. Na przykład, po ruchu mrówki M zamiast drogi BA pojawi się BC, zaś z punktu C ciąg dróg dotrze w punkcie D do dotychczasowej obwodnicy, która tym samym zmniejszy się.
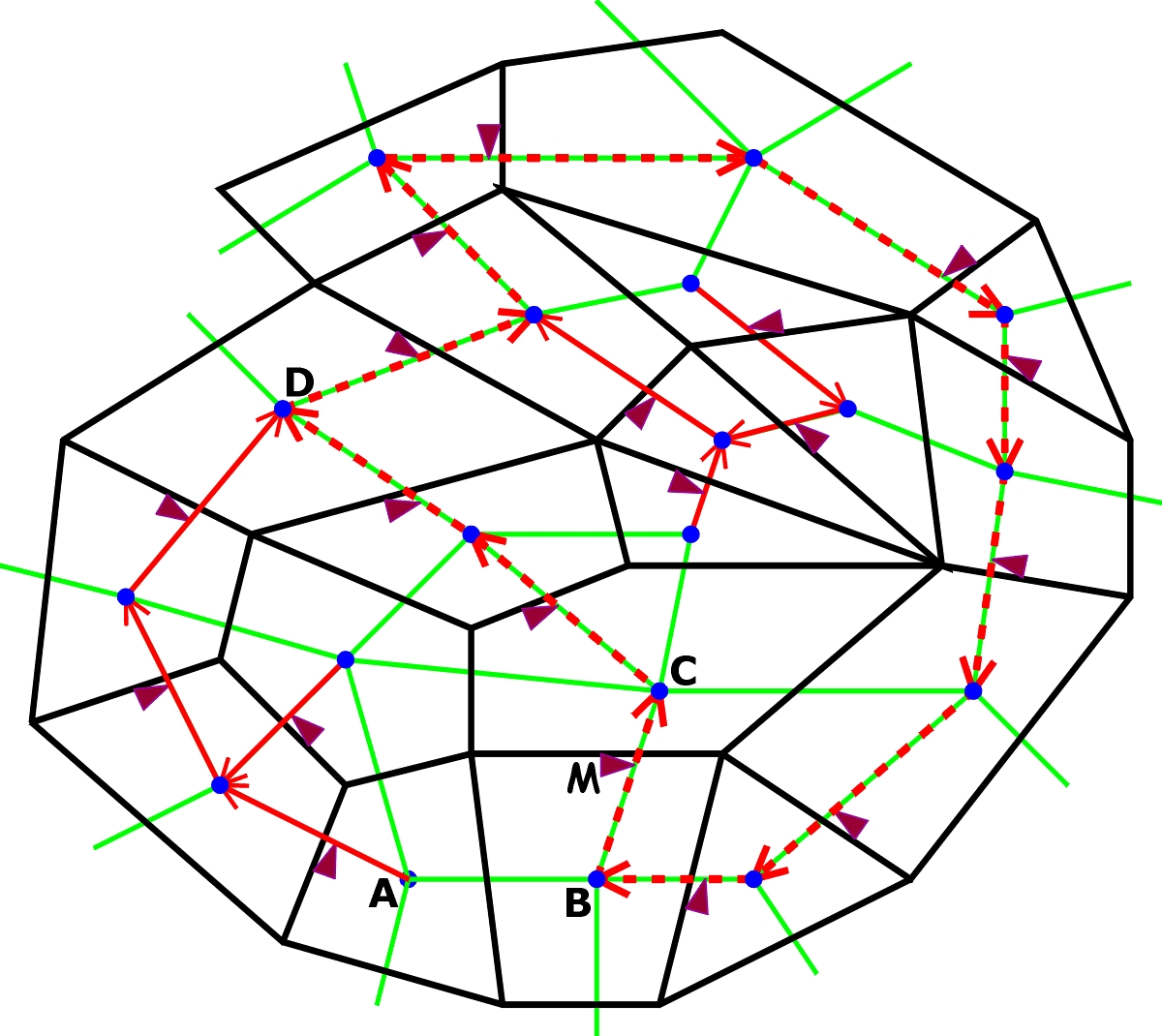
W ten sposób w następstwie ruchów mrówek „obwodnicowych” kolejne obwodnice otaczać będą coraz mniejszą liczbę krawędzi z mrówkami, aż liczba ta będzie tak mała, że spotkanie mrówek okaże się nieuniknione, co jest sprzeczne z przyjętym założeniem.

Komentarze
Ech… Panie Marku, nie mógł Pan swojego wpisu opublikować dopiero wieczorem. 😉 Wtedy bym zdążył przed Panem, a tak to Pan mnie wyprzedził. 🙁
Ale ponieważ w chwili ukazania się obecnego wpisu wszystko było już u mnie prawie gotowe, pozwolę sobie to również przedstawić (choć nie wiem czy w tym momencie kogokolwiek zainteresuje).
……………………………
Na wstępie chciałbym zaznaczyć, że przedstawiony przeze mnie poprzednio lemat wymaga pewnego uściślenia. Konkretnie dotyczy to dodatkowego założenia, że wewnątrz rozważanego zbioru wierzchołków nie ma „wysp” lub „dziur”, gdyż w tym przypadku nie musi on działać, tzn. nie gwarantuje konieczności podziału tego zbioru na mniejsze. Oczywiście w takiej sytuacji zbioru nie trzeba dzielić, bo niejako „podzielił się sam” i z lematu nie musimy korzystać (o czym zresztą wspominałem, rozważając osobno te dwa przypadki, we wcześniejszej wersji mojego dowodu).
Generalnie wymaga to jednak bardziej dokładnego rozpatrzenia tej sytuacji. Poza tym rysując „obrazki” w pewnym momencie stwierdziłem, że drugi z tych przypadków można „załatwić” nieco prościej. Dodatkowo nie dawał mi spokoju pojęciowy „potworek” 😉 , czyli „zwarty zbiór wierzchołków” wraz z niezbyt precyzyjnie z nim związanymi krawędziami, ścianami i mrówkami.
To wszystko skłoniło mnie do pewnego przebudowania dowodu, co przy okazji spowoduje (mam nadzieję), że stanie się on bardziej zrozumiały, ponieważ będzie się składać z serii krótkich (a więc chyba łatwiejszych do ogarnięcia) spostrzeżeń, a główna część dowodu będzie w postaci swego rodzaju algorytmu utworzonego również z krótkich kroków.
Oczywiście nie zamierzam tego tutaj przeprowadzac „od zera”. Będę jak najbardziej korzystać z tego co napisałem wcześniej (dla wygody link jest tu: http://penszko.blog.polityka.pl/?p=187#comment-17690), ale raczej odwołując się do poszczególnych punktów. Dlatego też, aby uniknąć nieporozumień, zastosowałem tu niezależną numerację.
……………………………
CZĘŚĆ PIERWSZA
Dla większej czytelności, wyjaśnienia skąd pochodzą opisywane spostrzeżenia wyróżniłem nawiasami kwadratowymi.
11.
Granica – tego określenia używać będę dla nieprzerwanej zamkniętej linii biegnącej w poprzek krawędzi zajętych w danym momencie przez mrówki, dzielącej wielościan na dwie części zwane dalej obszarami. Przykłady granic można zobaczyć tu: http://aps-projekt.pl/mrowki/mrowki20.gif (grube czerwone linie).
[definicja – a więc nie wymaga wyjaśnień]
12.
Wspomniany powyżej obszar będzie zastępował „potworkowaty” 😉 „zwarty zbiór wierzchołków”. W skład obszaru musi wchodzić przynajmniej jeden wierzchołek. Na poprzednim rysunku obszary oznaczono literami „X”, „Y”, „Z”.
[definicja]
13.
Mrówki tworzące granicę zmierzają wszystkie w tę samą stronę, tzn. albo wszystkie jednocześnie przechodzą z obszaru „X” do „Y” (jak na rysunku), albo odwrotnie.
[udowodnione w p. 9. poprzedniego komentarza]
14.
Granica nigdy nie styka, ani nie przecina się z inną. Jedyną możliwością podziału obszaru na mniejsze jest wyodrębnienie wewnątrz niego mniejszego obszaru – „wyspy”, o której dalej.
[wynika to z p. 13. – gdyby w jakimś punkcie schodziły się trzy (lub więcej) odcinków granic musiałyby istnieć obszary, na granicy których część mrówek przemieszczałaby się w jedną stronę, a część w drugą.]
15.
Obszar wyodrębniony z wielościanu przy pomocy dokładnie jednej granicy nazywać będę wyspą. Na rysunku z poprzedniego punktu warunek ten spełniają obszary „X” i „Z”. Oczywiście jeśli istnieje tylko jedna granica to zawsze obie części są wyspami, jednakże w momencie gdy wewnątrz którejś z tych wysp uda się nam wyodrębnić inny (mniejszy) obszar to wyspa ta traci swój status i staje się zwykłym obszarem.
[definicja]
16.
Dla każdej wyspy spełniony jest warunek: Kbm=W-1, gdzie W – liczba wierzchołków, Kbm – liczba krawędzi bez mrówek.
[udowodnione w pp. 4. i 5. poprzedniego komentarza; tu przypominam sprostowanie: lemat z poprzedniego komentarza jest prawdziwy, gdy wewnątrz nie ma mniejszych obszarów – czyli właśnie dla wyspy]
17.
W każdej wyspie każdy wierzchołek łączy się (przy pomocy krawędzi wolnych od mrówek) z dowolnym innym w dokładnie jeden sposób.
[wynika to z p. 16. w analogiczny sposób jak to przedstawiłem w p. 7. poprzedniego komentarza]
18.
Wyspę, wewnątrz której są tylko krawędzie bez mrówek nazywać będę drzewem (na rysunku obszar „Z”).
[definicja]
19.
Obszary, wyspy i drzewa otoczone granicą, na której mrówki maszerują w kierunku ich wnętrza będę określać jako typ „A”, a te, gdzie mrówki zmierzają na zewnątrz – jako typ „B”. Na rysunku obszar (drzewo) „Z” jest typu „A”, obszar (wyspa) „X” jest typu „B”, a obszar „Y” może być zarówno typu „A” jak i „B” – zależy od której strony będziemy go rozpatrywać (tzn. gdzie jest „zewnątrz”, a gdzie „wewnątrz”).
[definicja]
20.
Jeżeli gdziekolwiek zaistnieje drzewo „A”, to mrówki muszą się spotkać.
[sytuacja tak elementarna, że chyba nie wymaga dowodu – mrówki nie mają szans się minąć]
21.
Jeżeli gdziekolwiek zaistnieje drzewo „B”, to jest to sytuacja chwilowa i niepowtarzalna (wynika wyłącznie z początkowego położenia mrówek).
[rozumowanie analogiczne jak w p. 20.]
22.
Jeśli od momentu startu odczekamy odpowiednio długo, to drzew „B” nigdzie nie będzie.
[wynika to wprost z p. 21.]
Dalej będę rozpatrywać taką właśnie sytuację, tzn. po odczekaniu aż stan się „ustabilizuje” i minie wystarczająco dużo czasu aby móc prowadzić również analizę wsteczną.
23.
Jeśli do wyspy „A” wejdzie dodatkowa mrówka z granicy, to wyspa się zmniejszy,
[wynika to z p. 17. – krawędzie „bezmrówkowe” łączą wierzchołki na jeden sposób, a więc zajmując dowolną z nich (i nie zwalniając innej) tworzymy granicę w poprzek wyspy – sytuację przed tym manewrem można zobaczyć tu: http://aps-projekt.pl/mrowki/mrowki21.gif – cieńsze czerwone linie pokazują potencjalne przyszłe granice, które w tej chwili jednak nimi nie są, gdyż nie tworzą linii zamkniętej]
dalej pozostając jednak wyspą „A”.
[wynika to z p. 13. – kierunek ruchu wchodzącej mrówki powoduje, że ta część, do której zmierza będzie „domknięta” (a otworzy się pozostała część) – sytuację po tym manewrze można zobaczyć tu: http://aps-projekt.pl/mrowki/mrowki22.gif%5D
24.
Wyspa „B” może powstać tylko albo z mniejszej wyspy „B” (na skutek rozchodzenia się granicznych mrówek coraz bardziej na zewnątrz)
[rozumowanie analogiczne jak w p. 23. tylko analiza wstecz],
albo z obszaru „B” (z mniejszym obszarem wewnątrz) jako skutek ruchu mrówek wewnętrznych (powodującego likwidację tego mniejszego obszaru).
Gwoli ścisłości: tak naprawdę wyspa „B” nie ma w ogóle szans powstać – okaże się to później, z tym że wówczas będzie to już bez znaczenia.
25.
Wewnątrz każdej wyspy „B” musiał istnieć wcześniej jakiś obszar.
[wynika to z pp. 22. i 24. – gdyby wyspa „B” wyłącznie się rozrastała z mniejszej wyspy „B”, to analizując ten proces wstecz doszlibyśmy do drzewa „B”, a tego, po ustabilizowaniu się sytuacji, nie ma]
26.
Każdy obszar „B” zawiera lub zawierał w sobie mniejszy obszar.
[wynika to wprost z p. 25.]
27.
Każdy obszar „B” zawiera lub zawierał w sobie (niekoniecznie bezpośrednio) obszar „A”.
[wynika to z p. 26. – ponieważ KAŻDY obszar „B” zawiera w sobie mniejszy (i każdy jest skończony), to na końcu musi być przynajmniej jeden obszar „A”]
28.
Wielościan zawsze możemy podzielić na przynajmniej dwa obszary.
[wynika to z udowodnionego w poprzednim komentarzu lematu (w szczególności p. 7.) – zwracam tylko uwagę na to, że wielościan jako cały nie ma w sobie „dziur” i nie trzeba też rozważać budzącej wątpliwości „dodatkowej mrówki”, bo opieramy się wprost na wzorze Eulera w jego oryginalnej postaci]
……………………………
CZEŚĆ DRUGA
Dowód właściwy będzie, jak wspominałem na wstępie, w formie algorytmu:
101. START
Dzielimy cały wielościan na dwa obszary. [wykonalność gwarantuje p. 18.]
Z powstałych w wyniku podziału obszarów do dalszej analizy bierzemy „A” i przechodzimy do p. 102.
102.
Jeśli analizowany obszar jest drzewem to przechodzimy do p. 107.
Jeśli analizowany obszar jest wyspą (ale nie drzewem) to przechodzimy do p. 103.
W pozostałych sytuacjach przechodzimy do p. 105.
103.
Czekamy na ruch którejś mrówki (wewnątrz obszaru lub na jego granicy).
Jeśli będzie to mrówka graniczna przechodzimy do p. 104.
Jeśli nie (czyli poruszyła sie jedna z wewnętrznych) to sprawdzamy czy nasz obszar przestał być wyspą. Jeśli tak to przechodzimy do p. 105.
Jeśli nie (czyli nic istotnego się nie zmieniło) to powtarzamy ten punkt (czekamy na kolejny ruch).
104.
W wyniku ruchu mrówki granicznej otrzymujemy mniejszą wyspę „A”. [wynika to z p. 13.]
Wyspa ta staje się w tej sytuacji obszarem analizowanym i przechodzimy do p. 102.
105.
Analizowany obszar nie jest wyspą, a więc zawiera w sobie mniejszy obszar.
Jeśli ten mniejszy obszar jest typu „A”, to on staje się obszarem analizy i przechodzimy do p. 102.
Jeśli jest typu „B”, to przechodzimy do p. 106.
106.
Wewnątrz każdego obszaru „B” istnieje (lub istniał) obszar „A”. [wynika to z p. 17.]
Do dalszej analizy bierzemy ten właśnie obszar „A” i przechodzimy do p. 102.
107.
Analizowany obszar jest drzewem „A”, a w takim mrówki muszą się spotkać. [wynika to z p. 10.]
KONIEC ALGORYTMU
108.
Wykonując kolejne kroki tego algorytmu powodujemy, że analizowany obszar zmniejsza się (pp. 101., 104., 105., 106.) lub zachowuje swój rozmiar (p. 103.). Ta druga sytuacja nie może jednak trwać wiecznie ponieważ wymagałoby to unieruchomienia mrówek granicznych, a jak wiadomo wszystkie maszerują bez ustanku. Zatem analizowany obszar musi się stopniowo zmniejszać aż sprowadzi się on do drzewa (p. 107.), a tam, jak już napisałem, spotkanie musi nastąpić.
……………………………
I to by było chyba na tyle. Mam nadzieję, że teraz wszystko będzie zrozumiałe i nic nie będzie już budziło wątpliwości.
A za chwilę, po krótkim odpoczynku, przystępuję do analizowania dowodu Pana Marka. I teraz to ja się będę czepiać. 😉
Pozdrawiam
AB
Dziękuję za opublikowanie rozwiązania zadania o mrówkach.
Namysłu wymagały dwa zagadnienia:
1) Musi powstać obwodnica, gdzie mrówki schodzą się do wnętrza, które obwodzi (pkt. 5),
2) W którejś z kolejnych pozycji, obwodnica musi się „zacieśnić” (pkt. 6).
Nie widzę w rozwiązaniu żadnych słabości. Mnie ono przekonało.
Do Andrzeja69
Panie Andrzeju, jestem pełna podziwu dla Pana wnikliwości i wytrwałości w komentowaniu zadań i problemów pojawiających się w Łamiblogu. Sama dotąd nie ośmieliłam się wypowiadać na żaden temat, ale tym razem chciałam odnieść się w miarę delikatnie do Pańskiego ostatniego dowodu. Otóż mam obawę, że cokolwiek dobrego by o nim nie powiedzieć, ma on jedną wadę – jego obszerność niezbyt zachęca do lektury przeciętnego miłośnika łamania głowy. Próbowałam Pański dowód czytać ze zrozumieniem, ale po prostu nie dałam rady. Nie śmiem prosić o napisanie go w znacznie bardziej zwięzłej formie, zwłaszcza że nie wiem, czy jest to w ogóle możliwe, ale prosiłabym na przyszłość – sądzę, że także w imieniu innych miłośników Łamiblogu – w podobnych przypadkach o większą zwięzłość. Zapewniam równocześnie, że jeśli nie będzie to możliwe, nadal pozostanę wierną czytelniczką Pańskich wnikliwych komentarzy, podobnie jak blogu Pana Marka.
Przy okazji, przez dowód Pana Marka, choć znacznie krótszy, udało mi się „przebrnąć” także z niejakim wysiłkiem, ale wydaje mi się, że wszystko zrozumiałam. Nie jestem tylko do końca przekonana o tym, czy obwodnice rzeczywiście zawsze będą się zacieśniać, ale nie udało mi się znaleźć przykładu, który by przeczył temu stwierdzeniu.
Pozdrawiam wszystkich
Ewa
Panie Marku,
Przeczytałem z uwagą i przeanalizowałem dokładnie Pański dowód, a ponieważ wcześniej obiecałem, że będę się czepiać, to wypadałoby obietnicę spełnić… 😉
Zanim jednak do tego przejdę, chciałbym na moment nawiązać do mojej wersji. Komentując jej pierwotną postać (żeby nie było wątpliwości, dodam że nie chodzi mi tu o całkiem pierwsze moje podejście, czyli to z mrówką zastępczą – tamten dowód był całkowicie zły i do niego wracać nie będę – ale o obecną, tylko przed zawierającymi rysunki uzupełnieniami, a więc to: http://penszko.blog.polityka.pl/?p=187#comment-17502 ) napisał Pan bardzo dyplomatycznie, że „kilka fragmentów dowodu jest niejasnych lub przynajmniej wątpliwych” i równie dyplomatycznie, ale jednocześnie bardziej jednoznacznie 😉 , wspomniał Pan, iż „znajomi matematycy formułują tę opinię bardziej radykalnie”.
Zastanawiałem się, skąd to się wzięło. Pozwolę sobie (nie wiem, czy będzie trafne) na pewne zgadywanie. Generalnie matematyk (zakładając, że wykaże minimum dobrej woli i własnej inicjatywy) powinien sam dojść o co chodzi. Nawet jeśli nie wynika to w jasny sposób z opisu. W takiej sytuacji powie co najwyżej, że opis ów powinien być bardziej precyzyjny. Musiało zatem być coś, co mogło budzić poważniejsze wątpliwości. I rzeczywiście była tam pewna nieścisłość polegająca na tym, że dowodzony przeze mnie lemat nie gwarantował podziału, gdy wewnątrz rozpatrywanego zbioru wierzchołków znajdowała się – pozwolę sobie na skrót myślowy – wyspa.
Ten fakt nie powodował jednak tego, że cały dowód był zły. Po prostu pewną sytuację należało rozważyć osobno, natomiast ja, przyznaję, potraktowałem ją początkowo trochę po macoszemu.
Dowód ten wymagał zatem nie tylko bardziej klarownego wyjaśnienia, ale również pewnego uzupełnienia i to uchybienie, mam nadzieję, udało mi się usunąć w moim ostatnim komentarzu (to właśnie było głównym powodem dość znacznej zmiany jego postaci o czym zresztą tam wspominałem).
Zacząłem tę wypowiedź od mojej wersji, bo chciałbym dość nieśmiało zauważyć, że oba dowody znacznie więcej łączy niż dzieli.
Różnice są w szczegółach: np. granica-obwodnica u mnie jest zwykłą linią, a u Pana zbudowana jest z wektorów, co zdecydowanie upraszcza dowody pewnych zależności. Na pewno sposób, który Pan wymyślił, jest prostszy, łatwiejszy w zrozumieniu i bardziej elegancki. Nie zmienia to jednak faktu, że generalna idea jest w obu przypadkach taka sama. I tu, i tu pokazane jest, że:
1. Cały wielościan można podzielić na przynajmniej dwie części, takie że na całej granicy-obwodnicy wszystkie mrówki maszerują w kierunku jednej z nich.
2. W wyniku ruchu którejś z mrówek granicznych część, w stronę której mrówki idą zmniejsza się (aż zredukuje się tak, że spotkanie musi nastąpić).
3. Jeżeli wewnątrz rozważanej części pojawi się mniejsza „wyspa”, do której wnętrza mrówki zmierzają, to tę wyspę bierzemy do dalszej analizy.
4. Jeżeli wewnątrz rozważanej części pojawi się wyspa, z której mrówki rozchodzą się „na zewnątrz” (tzn. odwrotnie niż nasza rozpatrywana granica) to… Oj, chyba się rozpędziłem. To jest właśnie ta sytuacja, którą ostatnio uzupełniłem, a której brakowało w pierwotnym moim dowodzie i szczerze mówiąc nie widzę jej również u Pana.
Stąd też moje pytanie (oczywiście żartem 🙂 ): Panie Marku, dlaczego kopiuje Pan moje niedociągnięcia??? 😉
Zanim przejdę do rzeczy chciałbym wyraźnie zaznaczyć, że nie twierdzę, iż przedstawiony dowód jest zły (a wręcz przeciwnie – JEST JAK NAJBARDZIEJ POPRAWNY!), natomiast pewne mogące się zdarzyć sytuacje nie zostały rozpatrzone, a według mnie należałoby to zrobić.
Generalnie wątpliwości pojawiają się w punkcie 6. w dwóch miejscach:
1. „Zacieśnianie się” obwodnicy działa WYŁĄCZNIE w sytuacji, gdy w wewnątrz niej (rozumiejąc termin „wewnątrz” tak jak podano pod koniec p. 5.) nie ma innej. Pozornie jest w porządku, ponieważ powiedziane jest: „Wybieramy obwodnicę, wewnątrz której nie ma innej obwodnicy…”. Tyle, że może wystąpić taka sytuacja, w której nie ma obwodnicy nie mającej wewnątrz innej, jak np. tu: http://aps-projekt.pl/mrowki/mrowki30.gif .
2. Ciąg dalszy zacytowanego powyżej zdania brzmi: „…w następstwie ruchów w jej wnętrzu może pojawić się nowa obwodnica, wówczas na nią się przeniesiemy…”. Wyczuwam, że chodziło tu o sytuację, w której ta obwodnica jest zwrócona w tę samą stronę (tzn. jakby bardziej do wewnątrz). Pytanie tylko: A co się stanie, gdy ta obwodnica będzie zwrócona w drugą stronę, czyli w kierunku naszej rozważanej obwodnicy?
Podsumowując: Mimo tych dwóch nieścisłości dowód jako całość jest oczywiście prawidłowy, ale uważam, że powinien zostać uzupełniony.
A co inni na ten temat sądzą?
Pozdrawiam
AB
PS: W kwestii formalnej dotyczącej mojej wersji dowodu: Po tym jak zmodyfikowałem jego drugą część powinienem również skorygować część pierwszą, czyli lemat. Pozwolę sobie jednak tego nie robić, gdyż wydaje mi się, że wystarczająco opisałem co należałoby tam zmienić i osoby czytające (mające choć trochę chęci współpracy 😉 ) powinny same sobie z tym poradzić.
Do Envii:
Bardzo dziękuję za miłe słowa jak i za czytanie moich „wypocin” 😉 . Jednocześnie przepraszam, że mój dowód wyszedł taki długi i przez to niestety „niestrawny”. Na swoje usprawiedliwienie mogę jedynie powiedzieć to, że jego poprzednia wersja była zdecydowanie krótsza. Budziła ona jednak sporo wątpliwości. Być może wystarczyłoby dołączyć same rysunki (oraz pewne uzupełnienie), ale na wszelki wypadek wolałem ją trochę uszczegółowić. O tym, że liczyłem się z problemem i starałem się mu przeciwdziałać, świadczyć może to, że w nowym wywodzie unikałem dużych, litych bloków tekstu i przedstawiłem go w formie wielu, ale za to krótkich i łatwych do ogarnięcia, wyjaśnień.
Jeśli chodzi o zacieśnianie obwodnic w dowodzie Pana Marka, to proces ten następuje przy założeniu (o czym Autor wspomina), że wewnątrz rozważanej obwodnicy nie ma mniejszych i wynika z faktu, iż dowolna ściana znajdująca się wewnątrz tej obwodnicy wskazuje na jakąś inną. A więc albo ona, albo ta, na którą ona wskazuje, albo któraś z następnych w łańcuchu musi wskazywać na jedną ze ścian obwodnicy (na siebie nawzajem nie mogą, bo oznaczałoby to, że w środku jest mniejsza obwodnica). Stąd wniosek, że dowolna obwodnicowa mrówka wchodząc do środka „zamknie” mniejszą obwodnicę, a więc spowoduje „zacieśnienie”.
Osobno natomiast należałoby rozważyć przypadki, gdy wewnątrz rozpatrywanej obwodnicy znajduje się mniejsza. I tu według mnie byłoby wskazane dopowiedzieć parę zdań, aby dowód był kompletny (o czym napisałem w poprzednim moim komentarzu). Ale być może nie mam racji i wszystko jest ok, a ja się niesłusznie czepiam.
………………………….
Do Michała Gajzlera:
Przepraszam, że nie odpisałem wcześniej na zadane pytanie, ale starałem się najpierw „załatwić” mrówki całościowo, a to wymagało trochę czasu (którego niestety jak zwykle jest za mało).
Nie wiem czy po tak długiej zwłoce sprawa przedstawionego w Wikipedii dowodu tw. Eulera (i siatki wielościanu) jest dalej aktualna, ale spróbuję jednak nadrobić zaległości.
Użyte tam sformułowanie jest moim zdaniem dość nieszczęśliwe, bo z jednej strony rozcinanie tekturowego wielościanu rzeczywiście sugeruje siatkę, ale z drugiej, całe rozumowanie opiera się na tym, że każda ściana (mimo rozwinięcia na płaszczyźnie) dalej łączy się tymi, z którymi łączyła się w bryle. Tak naprawdę jednak kompletnie nie ma znaczenia czy wielościan jest z gumy i daje się rozciągnąć zachowując sąsiedztwo ścian, czy jest ze sztywnego materiału i ściany zachowują kształt tracąc ze sobą kontakt, pod warunkiem iż jednocześnie pamiętamy, które ściany ze sobą sąsiadowały i że odpowiednie pary krawędzi „zewnętrznych” są w rzeczywistości pojedynczymi krawędziami. Osobiście uznałem, że wersja „gumowa” jest bardziej zrozumiała.
Skoro już wróciłem do tego wątku, to jeszcze pozwolę sobie napomknąć, że w obecnej wersji mojego dowodu korzystam z tego rozumowania dwukrotnie. Osobno dowodząc możliwość podziału całego wielościanu na przynajmniej dwie części – tu można użyć wzoru Eulera wprost, tzn. W+S=K+2, który jest zawsze prawdziwy, a osobno w celu wykazania, że wejście mrówki granicznej do wnętrza obszaru spowoduje jego zmniejszenie, co oparłem na zależności między elementami wielościanu na tym obszarze. Tam jest ona postaci W+S=K+1 (co daje potem Kbm=W-1), wymaga jednak dodatkowego (pierwotnie przeoczonego) założenia braku „dziur”, tzn. sytuacji gdy ciąg krawędzi (lub całych ścian) „zatoczy okrąg” i połączy się z wcześniej rozważanymi elementami, ale jednocześnie bez uwzględnienia pewnego obszaru znajdującego się wewnątrz tego „okręgu”.
Oczywiście trzeba obiektywnie przyznać, że dowód tych dwóch rzeczy autorstwa Pana Marka (bez wzoru Eulera) jest bardziej elegancki, prostszy i łatwiejszy w zrozumieniu, ale z drugiej strony trudniejszy do wymyślenia. Wynika to po prostu z tego, że moja granica, jako zwykła linia, jest chyba bardziej intuicyjna (w znaczeniu wpadnięcia na pomysł, a nie czytelności gotowego rozwiązania) niż obwodnica stworzona z wektorów. No ale jak się nie ma, co się lubi, to się lubi, co się ma. 😉
Pozdrawiam
AB
PS: Dla obu osób, do których adresowany jest ten komentarz (do innych oczywiście też, ale jak na razie chyba nie było potrzeby) mam taką nieśmiałą propozycję (mam nadzieję, że nie urażę):
Ponieważ poza Gospodarzem, który występuje tu niejako oficjalnie (i któremu z racji pełnionej funkcji jak i stażu oraz pozycji w branży należy się szczególne traktowanie), wszyscy występujemy tu pod nickami (co z założenia niezbyt pasuje do oficjalnych zwrotów), to może by tak zrezygnować z tytułów „Pan” i „Pani” na rzecz bardziej bezpośredniej formy?
W każdym razie, niezależnie od innych opinii, wszystkich tych, którzy być może się krępują, jednostronnie „upoważniam” 😉 do zwracania się do mnie po imieniu. 🙂
Do Andrzeja69:
„może wystąpić taka sytuacja, w której nie ma obwodnicy nie mającej wewnątrz innej”
Czy taka sytuacja jest w ogóle możliwa?
Skojarzyło mi się to z rozyjską zabawką zwaną „matrioszką”, czyli „babą w babie”. Przecież zawsze jest jakaś najmniejsza baba, w której mniejszej już nie ma.
Może to trochę babskie myślenie, ale jednak chłopskie, czyli zdrowe:)
Pozdrawiam
zz
Do Zuzki:
Choć wydaje się to dziwne, ale taka sytuacja jest możliwa. Spowodowane jest to tym, że tutaj znaczenie słowa „wewnątrz” różni się od tego powszechnie przyjętego (oczywiście nieprzypadkowo i jak najbardziej słusznie).
Dlatego też proponowałbym przeczytać jeszcze raz drugi akapit w piątym punkcie dowodu Pana Marka, a potem spojrzeć na rysunek, do którego link zamieściłem w moim komentarzu. W przestawionej tam sytuacji każda z dwóch obwodnic jednocześnie znajduje się we wnętrzu drugiej!
Pozdrawiam
AB
Problem obwodnic, poruszony przez Andrzeja69, polegający na tym, że wewnątrz obwodnicy, w której mrówki schodzą się „do jej wnętrza” może znaleźć się obwodnica, w której mrówki schodzą się „na zewnątrz” proponuję rozwiązać w sposób następujący:
1) Jak obrazowo napisała Zuzka porównując obwodnice do matrioszek: musi być jakaś „najmniejsza”, tj. taka, w której innej nie ma.
(Przy takim podejściu musimy inaczej rozumieć „wnętrze” obwodnicy)
2) Krótko mówiąc: jeśli mrówki w tej „najmniejszej” obwodnicy schodzą się do jej „wnętrza” to ropatrujemy sytuację tak jak to opisał Pan Marek w „oficjalnym” dowodzie, tj. przewidując ewentualne przyszłe pozycje.
3) Natomiast jeśli w tej „najmniejszej” obwodnicy mrówki rozchodzą się „na zewnątrz”, to rozpatrujemy przeszłość, tj. pozycje jakie miały miejsce przed nastąpieniem aktualnie rozpatrywanej pozycji.
W obydwu przypadkach nastąpi owo kluczowe dla dowodu „zacieśnianie się” obwodnic. Z tym, że za pierwszym razem wnioskujemy, że spotkanie nastąpi w przyszłości, a w drugim, że musiało już mieć miejsce w przeszłości.
Do Andrzeja69:
Dziękuję za odniesienie się do zagadnienia siatki wielościanu.
Co do zwracania się do siebie: nie ma problemu.
Andrzeju, przeczytałam punkt 5, przyjrzałam się Twojemu rysunkowi i zgadzam się: każda „baba” jest w każdej „babie”.
Ale wnętrze żadnej baby nie jest we wnętrzu drugiej. Wydaje mi się więc, że wystarczy uzupełnić punkt 5 o warunek, żeby rozpatrywać obwodnicę, wewnątrz ktorej nie znajduje się inna obwodnica oraz jej wnętrze.
zz
Czy nie wystarczy udowodnić, że na czworościanie foremnym bez jednej ściany nie da się tych mrówek ustawić tak, by chodząc z jednakową prędkością się nie spotkały?
Uzupełnię swoją poprzednią wypowiedź:
Wystarczy znaleźć taką obwodnicę, która nie ma „na zewnątrz” lub nie ma „wewnątrz” innej obwodnicy. Nie interesują nas obwodnice, które mają i „wewnątrz” i „na zewnątrz” jednocześnie po choć jednej obwodnicy.
Dopiero wtedy patrzymy jak rozchodzą się na niej mrówki i rozpatrujemy albo przyszłe albo przeszłe pozycje.
Na rysunku Andrzeja69 można wybrać dowolną obwodnicę i rozpatrywać przeszłe pozycje (bo mrówki rozchodzą się „na zewnątrz”).
Helo
awesome post – i’m creating video about it and i will post it to youtube !
if you wana to help or just need a link send me email !