Zadanie czy łamigłówka?
Co różni łamigłówkę matematyczną od zadania matematycznego? Taki temat powraca co pewien czas w dyskusjach między miłośnikami rozrywek umysłowych. Stwierdzenie, że każda łamigłówka jest zadaniem, ale nie każde zadanie jest łamigłówką nie rozwiązuje sprawy, bo nie precyzuje, gdzie przebiega granica między zbiorami. Ponadto wypada uściślić, że chodzi o tzw. zadania podręcznikowe, a wówczas zbiór łamigłówek nie będzie częścią zbioru zadań, tylko oba zbiory będą miały co najwyżej jakąś część wspólną. Zadanie z podręcznika do matematyki nie jest łamigłówką – to również jest tzw. „też prawda”. Krótko mówiąc, wyraźnych różnic – pozwalających jednoznacznie określić, czy mamy do czynienia z zadaniem, czy z łamigłówką – nie ma, są natomiast cechy właściwe każdej z dwu form.
Rozwiązując zadanie korzystamy przede wszystkim z jakiegoś schematu, szablonu, wzoru, sprawdzając w ten sposób nabytą wiedzę. Natomiast na łamigłówkę patrzymy początkowo jak na twardy orzech, szukając miejsca, od którego najlepiej byłoby zacząć rozgryzanie, a potem próbujemy, czy to się uda. Główną rolę odgrywa pomysłowość, spostrzegawczość, umiejętność kojarzenia, wyobraźnia i kilka innych cech wiążących się z tzw. „instynktem łamigłówkowym” (termin wprowadzony przed kilku laty przez Marcela Danesiego, profesora semiotyki i etnolingwistyki Uniwersytetu Toronto).
W praktyce granica między obiema formami nie jest wyraźna, bo często w zadaniach występują cechy łamigłówkowe, a w łamigłówkach zadaniowe. Ponadto rzecz jest subiektywna – jeśli znam wzór, rozwiązuję zadanie, jeżeli go nie znam, zaczynam rozwiązywać łamigłówkę. Sudoku rozwiązywane po raz pierwszy jest znacznie bardziej łamigłówką, niż rozwiązywane po raz setny, gdy znamy i stosujemy, często niemal mechanicznie, gotowe sposoby. Zaczyna nią być, jeśli w trakcie rozwiązywania trafiamy na przeszkodę, zwłaszcza nietypową i musimy zacząć główkować, próbować, kombinować.
Większość starożytnych i średniowiecznych łamigłówek matematycznych nie jest dla nas łamigłówkami, choć była dla naszych przodków. Dziś rozwiązują je dzieci na lekcjach arytmetyki.
Jest siedem domów, w każdym siedem kotów, każdy kot łowi siedem myszy, każda mysz zjada siedem kłosów. Z każdego kłosa po wysianiu można otrzymać siedem porcji zboża. Ile porcji zboża zawdzięczamy wszystkim kotom z siedmiu domów? (papirus Rhinda, XVII w.p.n.e.).
Najstarsza siostra przychodzi do domu co 5 dni, średnia wiekiem co 4 dni, najmłodsza co 3 dni. Co ile dni wszystkie się spotykają? (Suang-Ching, IV w.).
Schody mają 100 stopni. Na pierwszym stopniu siedzi jeden gołąb, na drugim dwa gołębie, na trzecim trzy, na czwartym cztery, na piątym pięć i tak dalej aż do setnego. Ile jest wszystkich gołębi? (Alkuin, VIII w.).
Łamigłówkowe są natomiast nadal między innymi niektóre chińskie zadania sprzed wieków. Jedno z najstarszych i najbardziej znanych dotyczy pierwszego kwadratu magicznego.
Jak rozmieścić liczby od 1 do 9 w polach kwadratu 3×3, aby suma trzech liczb w każdym z trzech wierszy, w każdej z trzech kolumn i na każdej z dwu przekątnych była taka sama?
To przykład problemu, z którym można radzić sobie zarówno w sposób zadaniowy, jak i łamigłówkowy – w obu przypadkach po obliczeniu na wstępie, że sumy w rzędach będą równe 15.
Rozwiązując zadaniowo, wypisujemy wszystkie kombinacje trzech spośród liczb od 1 do 9, tworzące sumę 15. Jest ich osiem, czyli tyle, co magicznych rzędów w kwadracie.
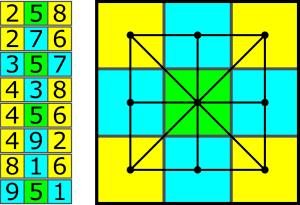
W środku kwadratu przecinają się cztery rzędy, a zatem w tym polu powinna znaleźć się jedyna liczba występująca czterokrotnie w wypisanych kombinacjach – piątka. W narożnych polach krzyżują się trzy rzędy, więc do nich trafią cztery liczby parzyste, bo każda pojawia się w kombinacjach trzy razy. Na podobnej zasadzie do kratek na bokach trzeba wpisać cyfry nieparzyste. Wszystko pasuje idealnie, a ponieważ kwadrat jest symetryczny, więc nie ma znaczenia, jak względem siebie ulokujemy na początku na przekątnych dwie kombinacje: 2-5-8 i 4-5-6; wpisanie czterech pozostałych liczb to już czysta formalność.
A teraz sposób bardziej łamigłówkowy.
Do umieszczenia w kwadracie mamy pięć liczb nieparzystych i cztery parzyste. Magiczna suma 15 jest nieparzysta, a więc mogą ją tworzyć tylko trzy liczby nieparzyste lub dwie parzyste i jedna nieparzysta. Inaczej mówiąc: w każdym z sześciu rzędów (przekątne na razie pomijamy) powinny znaleźć się albo dokładnie dwie liczby parzyste, albo żadna (warunek 2-0). Stąd wniosek, że dokładnie w jednym z trzech wierszy oraz dokładnie w jednej z trzech kolumn nie może być żadnej liczby parzystej. Możliwie są zatem trzy podstawowe rozmieszczenia cyfr parzystych (poniżej), z których tylko ostatnie spełnia warunek 2-0 dla przekątnych.

Suma liczb parzystych na każdej przekątnej powinna być taka sama, bo obie przecinają się we wspólnym środkowym polu, w którym powinna się znaleźć liczba dopełniająca tę sumę do 15. Teraz rozmieszczenie poszczególnych cyfr parzystych jest już trywialne, a pozostałe wskakują same.
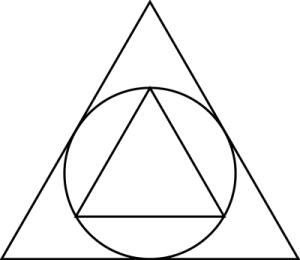
Na koniec wypada wspomnieć o charakterystycznym dla niektórych łamigłówek bodaj najciekawszym i najbardziej tajemniczym procesie rozwiązywania, znanym jako „zjawisko aha!”, czyli o… olśnieniu. To jednak temat na inne opowiadanie z pogranicza fenomenologii. Jego przedsmakiem niechaj będzie próba rozwiązania – bez obliczeń, najlepiej natychmiast – poniższego zadania.
W trójkąt równoboczny wpisany jest okrąg z wpisanym trójkątem równobocznym. Ile razy pole powierzchni dużego trójkąta jest większe od małego?

Komentarze
Panie Marku, rzec by można, wnioskując z Pan tekstu, że najprostsze sudoku dla wytrawnego sudokowicza w ogóle nie jest łamigłówką. Rozwiąże je niemal bezmyślnie i machanicznie. Czy zauważenie, bez wnioskowania, że czegoś brakuje w jakimś miejscu, jest już łamaniem głowy?
Może się mylę, ale uzupełnianie jakiegoś zestawu elementem, którego w nim brak, zawsze wymaga nie tylko spostrzegawczości, ale także wnioskowania logicznego. Czasem jest ono zawiłe, a czasem proste, ale zawsze jest.
Podoba mi się uwaga o przeplataniu się zadań matematycznych i łamigłówek. Rzeczywiście tak jest. A nawet stwierdziłam, że matematyczne przyzwyczajenia mogą być przeszkodą w rozwiązywaniu łamigłówek. Sama, gdy pachnie ona rachunkami, albo pytanie brzmi „Ile…?”, pierwszą rzeczą, jaką robię, jest sięganie po ołówek i liczenie. Po czasie widzę, że niepotrzebnie. Na przykład powyższe trójkąty z okręgiem: intuicyjnie wyczułam, że 4, ale że istotnie tak jest, przekonałam się po banalnych rachunkach. Dopiero po czasie odezwało się aha, miało jednak i tak matematyczną podpórkę, choć ołówka już nie potrzebowało.
Czasami jednak nie widzę
Chodzilo chyba o to, ze wystarczy trojkat ze srodka obrocic do gory nogami 🙂
Mnie interesują głównie staroźytne chińskie zad. textowe ;3