Samba na jednej cyfrze
Dla miłośników łamigłówek cyfrowych początek roku stanowi okazję do żonglowania oznaczającą go liczbą. Poza szukaniem jej niezwykłych własności matematycznych (dotychczas bez powodzenia) zabawy polegają na tworzeniu działań z tą liczbą związanych, a klasyczne zabawowe „konkurencje” są trzy.
W pierwszej powstają działania zawierające tylko cztery cyfry roku, bez zmiany ich kolejności. Wynikiem każdego następnego powinna być kolejna liczba naturalna. Mimo że wszelkie chwyty, nawet podwójna silnia, są dozwolone, zadanie bywa bardzo trudne. Oto kilka tegorocznych przykładów:
1 = 2^0 + 0 * 7
3 = sqrt(2 + 0 + 0 + 7)
11 = 2 + 0! + 0! + 7
15 = (-2 + 0 + 0 + 7)!!
23 = -((2 + 0!)!)!! + sqrt(0! + 7!)
Dotychczas wszystkie liczby od 1 do 24 udało się w ten sposób utworzyć; 25 jest pierwszą, która wciąż stawia opór.
Punktem wyjścia do drugiej konkurencji jest szereg cyfr:
1 2 3 4 5 6 7 8 9
Łącząc niektóre z nich (bez zmiany kolejności), czyli tworząc liczby oraz korzystając tylko ze znaków czterech podstawowych działań i z nawiasów, należy uzyskać wynik-rok. Z przykładów na czasie zapewne najłatwiejszy do odkrycia jest następujący:
(1 + 234 – 5 – 6 + 7 – 8 ) * 9 = 2007
Cała sztuka polega jednak na tym, aby znaleźć działanie z jak najmniejszą liczbą znaków, uwzględniając także nawiasy. W podanym przykładzie jest ich osiem. Czy może być mniej?
Trzecia konkurencja jest – jak Samba na jednej nucie Antonio Carlosa Jobima – grą na jednej cyfrze. Poza tym nie ma ograniczeń dotyczących znaków i symboli. Oto trzy ambitne przykłady sprzed trzech lat, autorstwa bardzo młodego (wówczas 17-latka) i bardzo obiecującego amerykańskiego matematyka pochodzenia rosyjskiego Borisa Alexeeva:
sqrt(2^22) – 2 * 22 = 2004
333 * 3! + 3! = 2004
6 * 6 * 6 * 6 + 6! – 6 – 6 = 2004
oraz jeden aktualny przykład, ale mało ambitny, bo dziecinnie prosty i łatwy do znalezienia:
999 + 999 + 9 = 2007
Wynik jest oczywiście tym lepszy, im mniej razy powtórzona zostanie cyfra.
Zachęcam Państwa do prób bicia rekordu Anno Domini 2007 w drugiej lub trzeciej konkurencji. A jeśli braknie czasu lub ochoty, to dla rozruszania szarych komórek proponuję krótki trening.
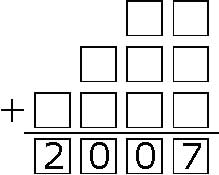
Wszystkie cyfry w trzech składnikach (zastąpione kratkami) są różne. Proszę rozszyfrować dodawanie, wiedząc że każda cyfra – pomijając zera – jest nie mniejsza od znajdującej się bezpośrednio nad nią.

Komentarze
Witam, ostatnia zagadka:
24+386+1597=2007
Panie Marku: pozdrawiam noworocznie Pana i wszystkich Łamigłówkowiczów ! PM
Oto układy od 1 do 9, niestety nie ma wśród nich rozwiązania z mniejszą ilością znaków niż 8.
((1 – 2 + 3 + 4) * 5 + 6) * 7 * 8 – 9 = 2007
((1 – 2 + 3 / 4 + 5) * 6 * 7 – 8 ) * 9 = 2007
((1 – 2) * 3 + 4 + 5) * 6 * 7 * 8 – 9 = 2007
(1 * 2 + 3 – 4 + 5) * 6 * 7 * 8 – 9 = 2007
(1 / 2 * 3 * 4 * 5) + 6 * 7 * 8 – 9 = 2007
((1 + 2 – 3 + 4) * 56 + 7 – 8 ) * 9 = 2007
((1 + 2 / 3) * 4 * 56 + 7 – 8 ) * 9 = 2007
((1 – 2) * 3 + 45 – 6) * 7 * 8 – 9 = 2007
(1 * 2 / 3 * 45 + 6) * 7 * 8 – 9 = 2007
(1 + 2 + 34 + 5 – 6) * 7 * 8 – 9 = 2007
(((1 + 23) / 4) * 5 + 6 ) * 7 * 8 – 9 = 2007
(12 + 3 – 4 – 5) * 6 * 7 * 8 – 9 = 2007
((12 * 3 – 4 + 5) * 6 – 7 + 8 ) * 9 = 2007
((12 * 3 – 4 – 5 + 6) * 7 – 8 ) * 9 = 2007
(12 / 3 / 4 + 5) * 6 * 7 * 8 – 9 = 2007
(1 * 2 / 3 + 45) * 6 * 7 + 89 = 2007
((1 + 2 + 34) * 5 + 67) * 8 – 9 = 2007
(1 * 23 * 4 – 56) * 7 * 8 – 9 = 2007
(1 *234 + 5 + 6 + 7) * 8 – 9 = 2007
(12 * 3 * 4 – 5 + 6 + 78) * 9 = 2007
((12 + 34) * 5 – 6 + 7 – 8 ) * 9 = 2007
Jeden przykład z minusem z przodu
(-1+2+345)*6-78+9=2007
Poniżej kilka przykładów od 9 do 1
(98/7+654)*3+2+1=2007
(9-8+7+654)*3+21=2007
(98+76-5)*4*3-21=2007
(9+87+6)*5*4-32-1=2007
(9*8*7-6+5)*4-3-2*1=2007
(9*8*7-6+5)*4-3-2/1=2007
Antyp
Dwie propozycje dla roku 2007
9!/(9*9+99)-9=2007
333*3!+3*3=2007
I jedna z trickiem
6!+6!+666-99=2007
99 to odwrócone 66, no ale skoro wszystkie chwyty dozwolone…
Antyp
Antypie, napisz proszę, czy zostawiłeś jeszcze coś rekordowego do znalezienia w konkurencji od 1 do 9. Bo jeśli korzystasz z jakiegoś sprytnego programu, który Twoim zdaniem wszystko wyłuskał, to szkoda czasu, żeby jeszcze się nad tym głowić.
Oto sześć znaków:
12*(34+56+78)-9 = 2007
pozdrawiam,
slawek
Mam jeszcze jedną propozycję:
50 +273+1684=2007
Sambę z jedną „przerzutką” znalazłam taką:
(6!! – 6) * 6!! – 9 = 2007
a bardziej grzeczną:
9!! + 9!! + 99 +9 + 9 = 2007
Pozdrawiam wszystkich noworocznie
Anka
Właściwie przykład podany przez Sławka jest odpowiedzią na moją prośbę do Antypa. Gratuluję Sławku – 6 znaków wygląda mi na rekord nie do pobicia, a nawet nie do wyrównania.
Zaskoczyło mnie także drugie rozwiązanie końcowej łamigłówki podane przez Ankę, bo trudno na nie wpaść.
Przepraszam, co oznacza zapis n!!?
Wyrazenie n!! oznacza podwójną silnię, czyli iloczyn wszystkich liczb naturalnych parzystych (dla n parzystego) lub nieparzystych (dla n nieparzystego) do n włącznie.
Teoretycznie istnieje też potrójna, poczwórna itd. silnia, ale należą one raczej do gabinetu osobliwości. W praktyce nawet podwójna stosowana jest rzadko.
Nie udało mi się Sławka przebić, ale wyrównać wynik tak.
1 + 2345 – 6*7*8 – sqrt9 = 2007
No to w takim razie 5 znaków 😉
12+345*6-78+sqrt9 = 2007
Tu jeszcze jedno rozwiązanie z 6 znakami, bez nawiasów:
1*2+345*6-7*8-9=2007
Nie wiem czy rozwiązania z pierwiastkiem kwadratowym mogą być
uwzględnione ponieważ p. Penszko w warunkach zadania napisał
„Łącząc niektóre z nich (bez zmiany kolejności), czyli tworząc liczby oraz korzystając tylko ze znaków czterech podstawowych działań i z nawiasów, należy uzyskać wynik-rok.”
Pozdrowienia Antyp
Tu jeszcze jedno rozwiązanie z 6 znakami, bez nawiasów:
1*2+345*6+7-8*9=2007
Do zadania z takimi samymi liczbami
((1+1)*111+1)*(11-1-1)=2007
(222+2/2)*(2+2/2)^2=2007
(sqrt(8^8)-88+8)/(sqrt(sqrt(8+8))-8/8=2007
Zbyszek
Pozdrowienia Antyp
cztery:
12/34*5678+sqrt9=2007
a swoją drogą ładnie wyglądałoby 2004 jako 12/34*5678
znalazlem 3 rozwiazania (bez 0)
24 + 386 + 1597 = 2007
43 + 275 + 1689 = 2007
34 + 275 + 1698 = 2007
a rozwiazanie
50 +273+1684=2007
no zgadza sie, ale zawiera 0
Ponieważ nikt nie ma śmiałości skorygować rozwiązań podanych przez Jerka, więc wypadło na mnie: rozwiązanie drugie i trzecie nie spełnia warunku podanego z ostatnim zdaniu – siódemka w liczbie 2007 jest mniejsza od cyfry znajdującej się nad nią.
Przy okazji: rozwiązanie Sławka z czterema znakami zasługuje na medal Fieldsa :).
mp
Czy ktoś zna wzór na silnię trójkątną?