Charlie i Amita
Ostatnio w Los Angeles dzieje sie coś dziwnego – zewsząd zieje nudą. Nikt nie próbuje nic ukraść, przemycić, ani tym bardziej nadszarpnąć komuś zdrowie lub pozbawić życia. Notoryczni przestępcy zgłaszają się jako wolontariusze do pracy w organizacjach dobroczynnych, oglądają kreskówki lub włączają się do akcji „Całe Los Angeles czyta dzieciom”. O powrót do zwykłej aktywności proszą ich agenci FBI zagrożeni utratą pracy.
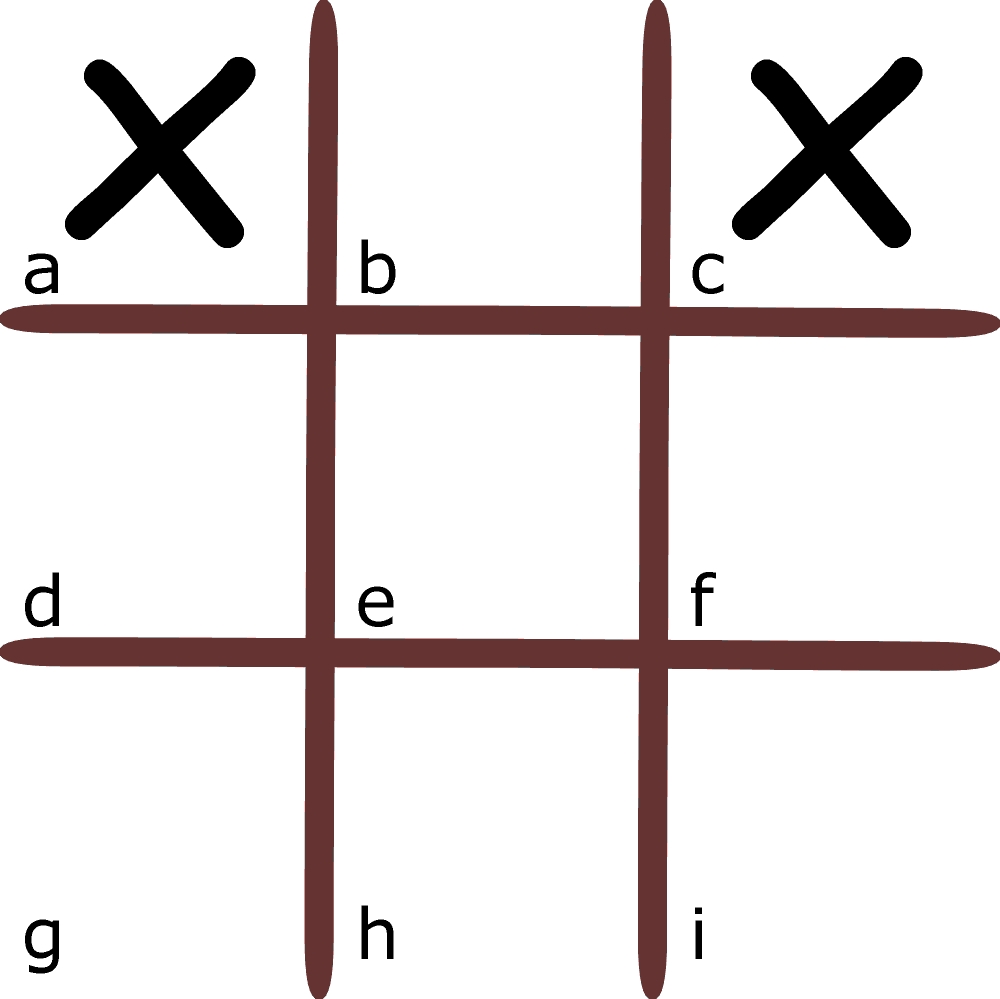
Nie wiadomo, skąd taka zmiana. Charlie Eppes i Amita Ramanujan – genialny matematyk i równie znakomita matematyczka, oboje ze scenki w poprzednim wpisie – próbują ustalić przyczyny tej nienormalnej sytuacji, a w przerwach grają w kółko i krzyżyk. Charlie stawia kółka, Amita krzyżyki. Na rysunku pokazana jest sytuacja po sześciu ruchach.
Jak widać ten, na kogo teraz przypada ruch, może wygrać. Kto nim jest?
Zakładamy, że dotąd oboje nie popełnili prostego błędu, czyli żadne z nich:
1. nie odpuściło sobie możliwości wygranej, jeśli taka się pojawiła;
2. nie zrezygnowało z zablokowania zwycięskiego ruchu przeciwnika, jeżeli wystąpiło takie zagrożenie.
W konkretnej sytuacji pierwsza z dwu powyższych ewentualności – jeżeli obie wystąpiłyby równocześnie – byłaby oczywiście priorytetowa, ponieważ kończyłaby grę.
W następnej przerwie w pracy nad ustaleniem wzoru matematycznego na przerażającą sielankę w Los Angeles, Amita zaproponowała kolejną partyjkę kółka i krzyżyka, ale tym razem wariantu z bardzo zmienionymi regułami: każdy może w jednym ruchu postawić jeden, dwa lub trzy swoje znaki, ale jeśli dwa albo trzy, to muszą się one znaleźć w tym samym rzędzie lub kolumnie; zwycięża ten, kto postawi ostatni, czyli dziewiąty znak. Jak widać reguła „trzy w rzędzie” nie ma w tym wariancie żadnego znaczenia.
Po pierwszym ruchu Amity sytuacja wyglądała tak:
Na którym polu lub polach umieścił w tym momencie kółko (kółka) genialny Charlie, jeśli ruchem tym zapewnił sobie zwycięstwo? Zakładamy, że w dalszej grze obie strony wykonywały najlepsze posunięcia.
Wśród osób, które poprawnie rozwiążą obie łamigłówki, rozlosowana zostanie nagroda – atrakcyjna gra planszowa. Jaka? To na razie pozostaje niespodzianką. Ujawnię tylko, że nazwa gry jest taka sama, jak nazwa miasta znajdującego się w odległości około 11750 kilometrów od Los Angeles.
Na przesyłanie odpowiedzi w formie komentarza do tego wpisu mają Państwo czas do czwartkowego południa (6 grudnia). Przed upływem tego terminu komentarze z rozwiązaniami nie będą oczywiście publikowane.
A następny konkurs z nagrodą – już 7 grudnia.

Komentarze
W 1-szym wygra Charlie (kółka)
W 2-gim Charlie musi postawić kółka na b, e i h. Jest to jedyny wygrywający ruch.
Wygląda na to, że będzie 2:0 dla Charliego.
W pierwszej łamigłówce, znakiem, który pojawił się jako ostatni, jest krzyżyk w polu „a”.
Dlaczego krzyżyk?
Gdyby ostatnim znakiem było kółko, musiałoby pojawić się w polu „f” – w związku z istniejącymi groźbami na „g” i „i” ruch ten nie mógł być obojętny (zasada nr 2) i jedynym powodem nie blokowania którejś z nich była obrona przed jeszcze jedną groźbą, możliwą tylko na wspomnianym polu „f”. Jeśli jednak cofniemy ten ruch, to okaże się, że ostatni w tej sytuacji krzyżyk zostałby postawiony wbrew zasadzie nr 1: bez względu na to, który by to był, zawsze wcześniej musiałyby istnieć dwa w linii z wolnym trzecim polem. Dochodzimy zatem do sprzeczności, a więc ostatnim znakiem musiał być krzyżyk.
A dlaczego w polu „a”?
Rozumując analogicznie jak poprzednio, wobec istniejącej (i nie sparowanej) groźby na polu „i”, musiał blokować jakąś inną, a ta była możliwa wyłącznie na „a”.
Z kolei ostatnim kółkiem, które pojawiło sie na planszy było to w polu „c”. Wcześniejsze ruchy mogły być już wykonywane w dowolnej kolejności.
Podsumowując: w zadanej pozycji ruch ma Charlie i wygrywa stawiając kółko w polu „i”.
W drugiej łamigłówce, jeśli Charlie chce być pewny wygranej, powinien umieścić trzy kółka w polach „b”, „e” i „h”. Amita ma wówczas dwie możliwości:
1. Stawia dwa krzyżyki w rzędzie lub kolumnie – wtedy Charlie wygrywa od razu umieszczając dwa kółka w ostatnim pozostałym rzędzie (lub kolumnie).
2. Stawia jeden krzyżyk – w tej sytuacji Charlie stawia również jedno kółko, ale tak, by nie znajdowało się ono w tym samym rzędzie ani kolumnie co ów krzyżyk. Powoduje to, że Amita nie może w następnym ruchu zająć na raz obu pozostałych wolnych pól i w związku z tym ostatnie z nich przypadnie Charliemu.
Inny sposób wygranej Charliego to umieszczenie jednego kółka na którymś z pól: „d”, „f”, „g” lub „i”, ale metoda podana powyżej jest zdecydowanie prostsza.
Jeśli chodzi o drugą grę, to uważam (zakładając, że się nie pomyliłem w analizie), iż przy prawidłowej grze obu stron zawsze powinien wygrać przeciwnik rozpoczynającego.
Na wstępie zauważmy, iż z uwagi na to, że przekątne nie biorą udziału oraz to, że dwa znaki możemy równie dobrze stawiać obok siebie jak i „rozstrzelone”, kolejność poszczególnych rzędów i kolumn nie ma znaczenia i możemy je w rozumowaniu dowolnie między sobą zamieniać (podobnie jak np. w pewnym stopniu w sudoku). Wniosek stąd taki, że rozpoczynający ma tak naprawdę tylko trzy różne ruchy: może postawić jeden, dwa lub trzy znaki. Natomiast to gdzie je postawi nie odgrywa żadnej roli.
Mamy więc trzy przypadki:
1. Rozpoczynający umieszcza dwa znaki (bez względu na ich położenie sprowadza się to wariantu jak w zadaniu) – odpowiadamy trzema znakami prostopadle.
2. Rozpoczynający umieszcza trzy znaki – odpowiadamy dwoma znakami prostopadle (w dowolnym miejscu) i otrzymujemy analogiczną sytuację jak powyżej.
3. Rozpoczynający umieszcza jeden znak – odpowiadamy stawiając dwa znaki, z tym że jeden z nich powinien się znaleźć w tym samym rzędzie lub kolumnie co znak już istniejący, natomiast drugi nie (uwzględniając uwagę zamieszczoną na końcu, odpowiada to alternatywnej metodzie wygranej Charliego). Dalej pozostaje do rozważenia 16 możliwych odpowiedzi, których nie będę tu analizować (bo byłoby to długie i nudne), jednakże po każdej z nich, przy najlepszej grze obu stron, ostatni ruch należy do gracza nr 2.
I na koniec jeszcze jedna uwaga (aczkolwiek bez wpływu na strategię): nie ma znaczenia jakie znaki gracze stawiają – właściwie to mogliby tylko jeden rodzaj.
Pozdrawiam
AB
1. Wygra Charlie.
2. Trzy kółka na polach b,e,h.
Ad.1. Ze wzgledu na dwie grozby X na g i h ostatnim ruchem musiał być X na polu a. A ruch wczesniej to O na polu c. Aha – gdyby zalozyc, ze widząc swoją przegraną gracz gra dowolnie -> możliwa byłaby odwrotna sytuacja: przedostatnim ruchem był X na a i teraz Amita widząc, że nie obroni się – gra „jakkolwiek” czyli O na c.
Ad.2. Po takim zagraniu Amita może:
– postawić dwa krzyżyki (na df, gi, dg, fi) -> wówczas Charlie dostawia brakujące dwa kółka.
– postawić jeden krzyżyk -> wówczas Charlie stawia jedno kółko „po przekątnej”, tj. np. jeśli Amita postawiła na f – Charlie stawia na g; Amicie pozostaje postawienie swojego krzyżyka i czekanie na ostatnie kółko Charliego.
Pytanie do ogladajacych serial regularnie (ja widzialem z 3 odcinki):
Czy panna Amita jest jakąś rodziną Tego Ramanujana? (potomstwem chyba być nie może…o ile pamietam)
1. Wydaje mnie się, że musiały zaczynać kółka i to one wygrają. Ostatnim postawionym kółkiem było to w górnym rogu, na co poszła odpowiedź w postaci krzyżyka w górnym rogu.
2. Charlie może postawić BEH i wtedy ta laska przegrywa. Bo może ona: postawić D (lub analogicznie G, F lub I). Wtedy Charlie I (lub analogicznie F, G lub D) i zostają dwa pola nie w jednej linii, a drugi ruch ma Charlie
Lub laska może dać DG (analogicznie FI), wtedy Charlie FI (lub DG),
albo dać DF (lub GI), a wtedy Charlie GI (lub DF)
w pierwszj zagadce wygrają kółka, a w drugiej wystarczy umieścić w środkowej kolumnie (pola b, e, h) trzy kółka
pozdrawiam
Pierwsza zagadka : Nastepny stawia kólko Charlie (na pozycji i) i wygrywa .
Uzasadnienie
Przyjmijmy , że ostatnim ruchem przed tym ułożeniem znaków było postawienie kólka – jeżeli to było kółko z pozycji b) albo c) to byłby to ruch nieprawidłowy , ponieważ należało zablokować na pozycji g) albo i) , jeżeli to było kółko z pozycji f) to poprzedni krzyżyk byłby postawiony nieprawidłowo , ponieważ można było wygrać .
A zatem ostatnim ruchem było postawienie krzyżyka . A żeby wszystko było zgodne z podanymi regułami , to przedostatnim ruchem było postawienie kółka na pozycji c) na co w odpowiedzi Amita musiała zablokować jedną z dwóch gróźb , na pozycji a)
Druga zagadka : Charlie powinien postawić trzy kółka w pozycjach b) , e) i h) . Jeżeli w odpowiedzi Anita postawi jeden znak krzyża to Charli odpowiada kółkiem po przekątnej i po następnym , wymuszonym jednym krzyżyku wygrywa . Jeżeli w odpowiedzi Anita postawi dwa krzyżyki to Charlie kończy grę dwoma kółkami .
Pozdrowienia
AC
Esteon:
Z informacji na temat serialu wynika, że bohaterka została nazwana po prostu na cześć jej rodaka; scenarzysci chyba nigdzie tego nie uzasadniają koligacjami rodzinnymi.
Sporo innych ciekawostek (po polsku) jest na stronie Filmweb.
mp
1. Amita
2. beh
Witam
Łamigłówki kółko-krzyżykowe.
1. Charlie zaczął partię i może ją wygrać, ale ciekawe, że może i dać wygrać.
2. Charlie umieścił kółka na polach: b, e, h.
Uwaga dotycząca nagrody.
Niespodzianką byłoby dla mnie, gdyby atrakcyjną grą planszową nie okazało(a) się PYLOS, bo istnieje pewne podobieństwo tej gry do jednej z konkursowych łamigłówek i odległość z „miasta aniołów” do greckiego miasteczka o nazwie Pylos jest zbliżona do podanej przez Pana Marka.
Pozdrawiam
Postanowiłem napisać parę słów trochę nie na temat, bo związanych z dwoma wcześniejszymi odcinkami: „Od tercetu do septetu” oraz „Sudoku kontra spam”. Pozwalam sobie zamieścić ten komentarz tutaj, bo po pierwsze: tam już pewnie nikt nie zajrzy, a po drugie: dotyczy on obu wpisów i trudno byłoby się zdecydować, do którego z nich go dołączyć. 😉
Jeśli chodzi o pierwszy tytuł to chciałbym nawiązać do „supertwardego orzecha” czyli kwintetu liczb pierwszych. Zadanie okazało sie rzeczywiście niełatwe, choć należałoby je raczej określić jako wyjątkowo pracochłonne (dla komputera oczywiście, bo sam algorytm był bardzo prosty). Dość powiedzieć, że napisany w tym celu program uruchomiony na jednym rdzeniu procesora Core 2 Duo 2.40 GHz podkręconego na 3.33 GHz używał ponad 1GB pamięci i potrzebował na to zadanie… ponad cztery dni (dobrze, że procesor jest dwurdzeniowy, a gigabajtowa kość RAMu ma braciszka bliźniaka, bo inaczej zostałbym uziemiony bez komputera 😉 ). No, ale w końcu udało się dotrzeć do wyników. 🙂
Kwintet tworzą następujące liczby: 11, 239, 11057, 21011, 62303. Każda z nich jest pierwsza, pierwsze są również wszystkie ich złożenia (nie będę tu wymieniać wszystkich dwudziestu kombinacji), oczywiście liczbą pierwszą jest także ich suma wynosząca 94621 i jest to najmniejsza liczba spełniająca warunki zadania (przy okazji potwierdzam, że 107 jest rzeczywiście najmniejszą sumą w przypadku tercetu, następne w kolejności są 239=3+7+229 i 331=3+137+191, dalej nie sprawdzałem, choć te obliczenia trwały ułamek sekundy).
Algorytm realizował zadanie metodą „brute force” analizując wszystkie możliwe kombinacje, co spowodowało, że jego koszt był rzędu n^5, stąd też taki długi czas obliczeń. Ciekaw jestem, czy można by to osiągnąć w jakiś bardziej subtelny sposób i dzięki temu mniej czasochłonny. To zagadka dla pozostałych główkołamaczy.
Warte uwagi jest również to, że samo sprawdzenie wyników (czyli 26 liczb – czy są pierwsze oraz jednego pięcioskładnikowego dodawania) odbyło się momentalnie.
Przechodząc do drugiego tematu muszę na wstępie zauważyć, że metoda zwalczania spamu przy pomocy łamigłówek zapowiada się bardzo ciekawie.
Aczkolwiek moim zdaniem akurat sudoku do tego celu nadaje się nie najlepiej. Uważam tak jednak nie dlatego, że łatwo o program rozwiązujący. Biorąc pod uwagę fakt, że komputery przecież nie myślą, a jedynie wykonują zaprogramowane działania, taki serwer e-mailowy po prostu MUSIAŁBY być wyposażony w odpowiedni program. Oczywiście nie w taki powszechnie dostępny (dla ludzi), bo z nim by się „nie dogadał”, ale w specjalne procedury wbudowane w system. Także łamigłówki obowiązkowo byłyby standardowe (co nie musi oznaczać wyłącznie wersji klasycznej). Inną możliwością byłoby dostarczanie łamigłówki oryginalnej, ale wraz z nią również odpowiedniej procedury rozwiązującej (bo inaczej komputer nawet nie ruszyłby z miejsca), ale stopień „trudności” byłby w tym przypadku taki sam: komputer nie będzie się „zastanawiać” jak podejść do problemu, tylko wykona odpowiedni, choć może nietypowy algorytm i tyle. Jeśli chcielibyśmy wydłużyć czas potrzebny na rozwiązanie, to raczej należałoby zwiększyć ilość kombinacji np. tworząc sudoku 16×16, 25×25, a może i 100×100 😉 .
Zauważmy zresztą, że ten czas wcale nie musi (a nawet wręcz nie może) być bardzo długi. Kilka sekund opóźnienia powinno wystarczyć. Utrzymywanie serwera wyłącznie po to (bo na nic innego nie starczy już mocy obliczeniowej), by wysłać raptem kilka tysięcy niechcianych e-maili w ciągu doby (to wbrew pozorom wcale nie jest dużo) po prostu się nie kalkuluje. Natomiast wspomniane opóźnienie nie może być za długie, bo jakbyśmy się sami czuli, gdyby po nadaniu przez nas e-maila coś nam blokowało NASZ komputer na kilka minut?
Dlaczego w takim razie nie sudoku? Otóż nie z powodu zbyt łatwego lub zbyt trudnego rozwiązywania, ale z powodu zbyt trudnego (czyli czasochłonnego) układania łamigłówki (w stosunku do czasochłonności poszukiwania wyniku). Oczywiście, wiem, że stosowne programy potrafią je tworzyć w tempie ekspresowym, ale tak samo, a podejrzewam, że nawet szybciej, je rozwiązują. A jeśli skomplikujemy je, by spowolnić rozszyfrowanie, to odbije się to również na ich układaniu. Poza tym, może się mylę, ale wydaje mi się, że podczas tworzenia sudoku jest wskazane jego „robocze” rozwiązanie (lub jakaś inna, ale niekoniecznie szybsza, adekwatna procedura) mające na celu sprawdzenie poprawności łamigłówki. Myślę, że na ten temat, Pan, Panie Marku, jako profesjonalny twórca łamigłówek (mam nadzieję, że tym określeniem nie urażę), mógłby mieć zdecydowanie więcej do powiedzenia.
Co w takim razie w zamian i co ma wspólnego pierwszy wątek z drugim?
A no to, że liczby pierwsze doskonale nadają się do takich łamigłówek.
Złośliwe myśli mnie nachodziły 😉 , gdy mając świeżo w pamięci tekst o spamie, widziałem jak mój komputer się męczy z prostą przecież w sformułowaniu (zarówno treści jak i algorytmu) i, jak już napisałem wcześniej, szybką w sprawdzeniu poprawności rozwiązania, łamigłówką. Hmm… podesłać coś takiego spamerowi (nawet załączając program) i… na kilka dni mamy delikwenta z głowy. 🙂 🙂 🙂
To oczywiście żart, ale samo wykorzystanie liczb pierwszych już nie.
Łamigłówka mogłaby wyglądać np. tak: komputer kodujący wybiera dwie duże (np. parudziesięciocyfrowe) liczby pierwsze, a następnie mnoży je przez siebie i wysyła iloczyn. Zadaniem komputera rozwiązującego jest operacja odwrotna: na podstawie otrzymanego iloczynu odnaleźć czynniki. A to okazuje się dużo bardziej czasochłonne (w końcu rząd wielkości iloczynu jest równy sumie rzędów czynników lub nawet o jeden od niej większy). A poza tym, co równie ważne, „łamigłówka” taka jest prosta w zdefiniowaniu i przy całkowicie powtarzalnej treści ogólnej możemy bez problemu uzyskać dowolną liczbę konkretnych „zagadek”. A że są one pozbawione wszelkich cech twórczych i ogólnie mało ciekawe dla człowieka… cóż, w końcu nie dla niego byłyby przeznaczone. A komputery przecież i tak tylko liczą, więc dla nich będą akurat.
Tego typu komputerowych „łamigłówek” można wymyśleć sporo więcej. Zainteresowanym podobnymi zagadnieniami polecam artykuł w Wikipedii: http://pl.wikipedia.org/wiki/Funkcja_jednokierunkowa.
Pozdrawiam
AB
Do Andrzeja69
Ponad cztery dni poszukiwania pięciu odpowiednich liczb, to robi wrażenie.
Ciekawe jak długo trwałoby szukanie siedmiu, dziewięciu, … , odpowiednich liczb i czy takich liczb jest nieskończenie wiele czy jest ich tylko skończona ilość.
Gratuluję cierpliwości!
Andrzej69:
Dzięki Panie Andrzeju za bardzo ciekawy i wnikliwy komentarz. Do poruszonych przez Pana spraw zamierzam powrócić w jednym z najbliższych wpisów.
Tymczasem gratuluję znalezienia „pierwszego” kwintetu, choć mam coś w rodzaju wyrzutów sumienia, że zafundowałem Pańskiemu komputerowi tak gigantyczną harówkę.
Określenie „profesjonalny twórca łamigłówek” jest miłe, ale mocno przesadzone. Układanie znanych rodzajów zadań, np. krzyżówek, sudoku lub podobnej „japońszczyzny” trudno nazwać twórczością, może rzemiosłem.
Natomiast „twórcą”, czyli autorem łamigłówek nowych, oryginalnych bywa każdy miłośnik gimnastyki umysłowej. Moim zdaniem to nie profesjonalizm (i bardzo dobrze), raczej efekt zamiłowania i natchnienia. Trochę mi się kojarzy wymyślanie łamigłówek z pisaniem poezji i Norwidowskim: „poetą się nie jest, poetą się bywa”.
Pozdrawiam
mp
pierwsze zadanie: ZACZĘŁY KÓŁKA
nie będę się chyba rozpisywał, jak do tego doszedłem… „żeby język giętki…..”
drugie: powinien postawić B E H. Wtedy zostają 2 lub 4 ruchy… w każdym razie liczba parzysta (wygrywająca)
1.) Teraz stawia ruch Charlie (kolka). Poprzedni ruch byl to ruch Amity w lewy gorny rog.
2.) beh. Amita może postawić jeden lub dwa znaki. Jeżeli postawi jeden, to Charlie stawia również jeden po stronie przeciwnej (dgfi). Jezeli postawi dwa (dg lub fi), to Charlie stawia rowniez dwa i wygrywa.
Pozdrawiam
Nie rozumiem stwierdzenia:
‚Jak widać reguła „trzy w rzędzie” nie ma tym wariancie żadnego znaczenia.’ Czy mógłby Pan to wytłumaczyć?
W tradycyjnym kółku i krzyżyku wygrywa, kto pierwszy postawi trzy swoje znaki w rzędzie. W tym wariancie chodzi o coś zupełnie innego, więc to, czy gdzieś się pojawi rząd trzech jednakowych znaków, nie jest istotne. (mp)
Przepraszam z góry za niezrozumiałe dla niektórych rozmowy 🙂
Do Andrzeja69
Jeżeli koszt był n^5 to gratuluje wygrania miliona dolarów :>
A tak poważnie to koszt byłby n^5, gdybyś miał górne oszacowanie, gdzie ten kwintet znajdziesz. Poza tym sprawdzasz tylko liczby pierwsze, których jest jest O(n/log n), i do tego jeszcze ciężko oszacować realny czas działania (jest to wręcz niemożliwe do zrobienia teoretycznie), skoro zapewne używałeś pruningu (wczesnego odcinania możliwości).
A co do zużytej pamięci – robiąc sito erastotenesa wystarczy 1 bit, a nie bajt i np. można nie sprawdzać liczb parzystych, no ale mając tyle ramu rozumiem, że się nie przejmowałeś 🙂
Program robiący sudoku działa nieporównywalnie więcej z rozwiązującym go, ponieważ działa on tak, że generuje (od zera) jakieś poprawne sudoku, a następnie zabiera po jednej cyfrze patrząc, czy dalej jest rozwiązywalne. 99% programów robiących sudoku właśnie tak działa (generuje się takich 10K a następnie inny program rozwiązujący – używający logiki – sprawdza, które z tych zadań pasują do oczekiwanego stopnia trudności itp itd).
Teoretycznie jednak argument za tym, że sudoku się generuje dłużej, jest żaden – bo nie trzeba za każdym razem generować nowego, albo ma się bazę danych albo można stworzyć nowy z istniejącego – permutując bloki, poziome, pionowe, obracając dodając cyfrę.
Rozwiązanie na spamerów (wg mnie dużo lepsze i niektórych podobnych miejscach gdzie trzeba sprawdzić czy „przy komputerze siedzi człowiek” (tzw test turinga) już wykorzystywane) jest tzw. testowanie semantyczne – sprawdza się rozumienie językowe/logiczne rozumowanie. Na przykład rysunek i pytanie, ile jest kwiatków na łące. Plus jest ten, że „komputer” sobie z tym nigdy nie poradzi, jeśli nie będzie miał zbioru wszystkich pytań, co z kolei jest bardzo czasochłonne dla samego człowieka.
1. Charlie wygrywa
2. b, e, h
Pozdrawiam
MK
1. Zaczęły i wygrywają KÓŁKA, czyli Karolek
2. Karolek zajmuje całą środkową kolumnę, czyli b-e-h – i po sprawie!
najpierw druga zagadka:Charlie umieścił kółka na polach b, e, h. pozostały 4 pola wolne: d,g,f,i. Anita mogła postawić : 1) 2 krzyżyki w rzędzie lub kolumnie. potem Charlie pozostałe dwa.
2) 1 krzyżyk np. d, wtedy Charlie też 1 w i. dalej Anita może tylko 1, a 1 zostaje dla Charliego.
Pierwsza zagadka:
Na pewno nie zaczynała Anita. Mogłaby być sytuacja nast:
X6,O3,O5 X6,O3,O5 X6,O1,O5 X6,O1,O5
X4,X2,O1 albo X2,X4,O1 albo X4,X2, O3 albo X2,X4,O3 Wtedy wygrałby Charlie, ale nie sądzę, zeby Anita tak stawiała krzyżyki. nie miałaby szansy na wygraną
Pierwsze zadanie: Gdyby z planszy usunąć wszystkie kółka, Amita (krzyżyki) miałaby trzy możliwości utworzenia rzędu ze swoich znaków. Te trzy możliwości nie powstały w jednym momencie – choć jedna z nich musiała istnieć przed ostatnim ruchem Amity. Teraz możemy spojrzeć na kółka – i już wiemy, która możliwość Amity istniała wcześniej – ta, którą Charlie zablokował. Tak więc ostatni krzyżyk postawiony przez Amitę, to ten w lewym górnym rogu. Tworzy on dwie możliwości wygrania partii, z których żadna nie jest zablokowana. Dlaczego? Jedyna możliwa odpowiedź brzmi – dlatego, że Charlie nie miał ku temu jeszcze okazji, ten krzyżyk to jednocześnie ostatni wykonany w partii ruch. Czyli teraz ruch należy do Charliego i to on wygrywa tę partię. Drugie zadanie: Charlie musi postawić trzy kółka w środkowej kolumnie diagramu (b-e-h). W ten sposób tworzy symetryczny układ wolnych pól i wystarczy mu małpować ruchy Amity. Jeśli ona zapełni dwa z tych czterech pól, Charlie zapełni pozostałe. Jeśli Amita postawi tylko jeden krzyżyk, Charlie też postawi jeden (dbający tylko o to, żeby nie zostawić dwóch wolnych pól w rzędzie lub kolumnie). Charlie ma zapewnione zwycięstwo.
odp. na pierwszą zagadkę – ruch przypada na Charliego (kółka).
odp. na drugą zagadkę:
XOX
_O_
_O_
czyli trzy kółka w środkowej kolumnie.
Do Andrzeja:
Jestem prawie pewny, że takich liczb jest nieskończenie wiele, bo w końcu, jeśli w ogóle istnieją, to co miałoby je limitować.
Natomiast ile trwałoby poszukiwanie septetu, nie mówiąc już o nonecie czy większych zbiorach, wolę nawet nie myśleć. Podobnie jak o poszukiwaniu kolejnego kwintetu.
Dziękuję za gratulacje cierpliwości, ale należą się one co najwyżej komputerowi (choć dla niego to akurat nic specjalnego 😉 ).
Napisanie programiku (plus dwie małe poprawki „po drodze”) to w sumie chwila. A potem już tylko zapuścić i… robić swoje, co najwyżej co jakiś czas spoglądając, czy coś się nie „wykluło” 😉 .
Pozdrawiam
AB
Do Pana Marka:
Myślę, że wyrzuty sumienia (jak również „coś w ich rodzaju” 😉 ) są całkowicie zbędne. W końcu komputer jest cierpliwy i pracowity i taka jego rola. Gdy sobie trochę popracuje, to mu nie zaszkodzi, a przy okazji będzie to dobry test na jego wytrzymałość. 😉
Jeśli chodzi o układanie łamigłówek, to chyba (nie mam własnych doświadczeń) zgodzę się ze stwierdzeniem, że dużo w tym rzemiosła, choć podobnie jak każde inne rzemiosło zawsze może być wykonywane lepiej lub gorzej (tu wspomnę choćby niedawny Pański wpis dotyczący krzyżówek), a między mistrzowskim rzemiosłem a twórczością granica już cienka i płynna. Poza tym, to z tego co mi wiadomo, wymyślił Pan jednak sporo oryginalnych łamigłówek, które może i nie były takimi światowymi hitami jak sudoku, ale uważam, że na miano twórczości zasługują.
W pełni się zgadzam z „bywaniem” twórcą. Żeby stworzyć coś ciekawego i oryginalnego niewątpliwie potrzebne jest natchnienie i zamiłowanie (to drugie uważam jako warunek absolutnie niezbędny, jeśli chcemy cokolwiek robić dobrze, a nie odwalać miernotę), a poza tym, przypuszczam, sporo… po prostu szczęścia.
Ale, jak to mówią, „dobrym szczęście sprzyja”. 🙂
Pozdrawiam
AB
Do Psyho:
Szczerze mówiąc niezbyt kojarzę o co chodzi z tym milionem dolarów. Gdybyś mógł mnie oświecić… Wiesz, taka sumka na drobne wydatki przydałaby się. W końcu święta idą… 🙂
A na poważnie:
Programik został napisany wyjątkowo ekstensywnie. Po pierwsze: z lenistwa, po drugie: miałem nadzieję, że poszukiwany kwintet znajdzie się stosunkowo prędko (tzn. suma nie będzie taka duża). Założenie takie przyjąłem po wcześniejszym przetestowaniu programiku dla tercetu, gdzie, jak już pisałem, nie tylko pierwszy, ale i dwa następne były stosunkowo niewielkie (trzycyfrowe) i znalazły się w ułamku sekundy. Algorytm oparty został na pięciokrotnej pętli w pętli. Najbardziej na zewnątrz potencjalne sumy, a następne – cztery pierwsze składniki (piąty wychodził już oczywiście z różnicy).
Nie bawiłem się też w oszczędność pamięci i tablica określająca, które liczby (w zakresie miliarda) są pierwsze była typu boolean. Na to akurat mogłem sobie pozwolić.
Ale jako ciekawostkę powiem, że po pierwszym wysypaniu się programu na przekroczeniu zakresów (gdy suma zbliżyła się do 53000), widząc że może zachodzić potrzeba kilkukrotnego ponownego uruchomienia, postanowiłem nie przeliczać sita Erastotenesa za każdym razem po starcie programu, tylko, aby było szybciej, zapisać jego wyniki na dysku. I tu, ze względu na dużo wolniejsze operacje dyskowe, nie tworzyłem już gigabajtowego pliku, ale upakowałem liczby pierwsze po jednej na bit i oczywiście z pominięciem parzystych, dzięki czemu miał on tylko 64MB.
Pisząc o koszcie rzędu n^5 miałem na myśli to, że tak wzrasta ilość obliczeń w miarę sprawdzania kolejnych liczb jako kandydatek na sumę kwintetu, a nie o wstępne, odgórne szacowanie czasu pracy programu, nie wiedząc jak wielka będzie owa suma. Masz jak najbardziej rację: sprawdzałem wyłącznie liczby pierwsze (a nie wszystkie po kolei), ale pisząc n^5 zrobiłem po prostu pewien skrót myślowy: n oznacza nie tyle samą sprawdzaną liczbę, ale liczbę liczb pierwszych nie większych od niej.
No i jeszcze jeden dodatkowy problem związany z szacowaniem czasu, o którym również wspomniałeś, to fakt, że jeden przebieg drugiemu nie jest równy. Czyli np. gdy dwa pierwsze składniki sumy po ich zestawieniu obok siebie nie tworzyły liczby pierwszej, to oczywiście nie przeliczałem już kolejnych wewnętrznych pętli dla następnych dwóch itp.
Ale chciałbym tu zaznaczyć, że nie chodziło mi o dokładne ani nawet przybliżone określanie czasu, tylko o podanie pewnej zgrubnej szacunkowej zależności: jak mocno wydłuża się potrzebny czas, gdy okazuje się że poszukiwana liczba jest większa niż zakładaliśmy.
Jeśli chodzi o sudoku, to brałem pod uwagę, że można korzystać z gotowej bazy, ale tu mogą być inne problemy. Np. jeśli byłaby to baza ogólnie dostępna, to mógłby z niej korzystać również komputer spamujący i mieć bazę gotowych rozwiązań itp.
Ale generalnie metoda „łamigłówkowa” nie musi być zła, natomiast uważam, że są lepsze sposoby jej realizacji niż akurat sudoku. Podejrzewam, że pozytywna odpowiedź na pytanie o jego przydatność dana przez autora tej koncepcji, była spowodowana raczej ukłonem w stronę pytającego niż praktyczną analizą tego problemu.
Przechodząc do zaproponowanego przez Ciebie zabezpieczenia antyspamowego to, o ile dobrze zrozumiałem, miałoby ono polegać na tym, że nadawca e-maila miałby sam, osobiście, jeszcze odpowiadać na jakieś pytanie i na tej podstawie drugi komputer mógłby stwierdzić, czy za komputerem siedzi człowiek czy nie. Przypomina mi to trochę metodę stosowaną przy rejestracji na różnych serwisach, zakładaniu kont e-mailowych itp., gdzie musimy przeliterować napis pokazany w postaci bitmapy.
Niestety, wydaje mi się, że i ono posiada pewne wady. Po pierwsze: mielibyśmy do wykonania jeszcze jedną dodatkową czynność, co czasami, w pośpiechu, mogłoby być bardzo denerwujące (w szczególności, że łatwo wówczas o pomyłkę w odpowiedzi), a po drugie nie każda automatycznie wysyłana poczta jest spamem.
Pozdrawiam
AB
Wiadomość z ostatniej chwili dla zainteresowanych liczbami pierwszymi: 😉
Dziś rano „padł” drugi kwintet, który tworzą liczby: 19, 8929, 12577, 30427 i 61129 w sumie dające 113081.
Ciężko mi jest tym razem powiedzieć, ile to trwało, bo komputer miał przerwy, ale myślę, że niewiele krócej niż w przypadku pierwszego.
Jeszcze chwilę wcześniej odpowiadając Andrzejowi napisałem, że nie chcę nawet myśleć, ile zajęłoby poszukiwanie następnego. Podejrzewałem, że będzie się on znajdować dużo dalej.
Ale programik pracował nadal, choć tym razem bardziej po to by NIE znaleźć.
Po prostu wcześniej, tak mniej więcej w połowie pierwszego etapu poszukiwań, widząc jak to długo trwa uruchomiłem na drugim komputerze (w pracy) ten sam programik, ale każąc mu sprawdzać sumy począwszy od 120000. Po pojawieniu się pierwszego kwintetu zatrzymałem go (sprawdził sumy raptem do 126000 niczego oczywiście nie znajdując) i nie planowałem już dalszego szukania, ale nie dawała mi spokoju luka pomiędzy 94621 (pierwszy kwintet), a wspomnianymi 120000. To trochę tak, jakby zostawić niedokończoną pracę. 😉
Dlatego też, żeby móc spokojnie powiedzieć, że sprawdziło się pełny zakres do 126000, zapuściłem jeszcze raz mój programik począwszy od miejsca, w którym wcześniej skończył i planując przerwanie jego pracy po osiągnięciu 120000. Generalnie nie wierzyłem, że coś w tym zakresie znajdzie – zrobiłem to wyłącznie dla porządku.
A tu niespodzianka. 🙂
Pozdrawiam
AB
PS: Oczywiście programik pracuje nadal, dopóki nie „wypełni luki”.
Andrzej powiedział:
„Niespodzianką byłoby dla mnie, gdyby atrakcyjną grą planszową nie okazało(a) się PYLOS”
Też bym się zdziwił jakby nie o Pylos tu chodziło.
Jedyne co mi przychodziło do głowy to Carcassonne, ale to jest około 9000 km tylko.
To ani nie Pylos, ani nie Carcassonne. Jednak jeśli ktoś trafi, to nie ujawnię tego przed oficjalnym werdyktem, który nastąpi po zakończeniu drugiego łamigłówkowego konkursu – a ten pojawi się tuż po najbliższej północy (mp)
Mała uwaga do odpowiedzi na drugą zagadkę:
Przestawiona przez chyba wszystkich metoda na zwycięstwo Charliego (czyli ruch „b-e-h”) jest niewątpliwie prawidłowa i najprostsza, ale wcale nie jest jedyna!
Charlie wygrywa również zawsze (choć gra może być dłuższa) stawiając jedno kółko na polu „d” lub „f” lub „g” lub „i”. Amita ma wówczas 16 różnych odpowiedzi: może postawić trzy krzyżyki na 2 sposoby, dwa krzyżyki na 8 sposobów i jeden krzyk na 6. Jeśli postawi trzy lub dwa krzyżyki, a także w dwóch sytuacjach gdy postawi jeden, Charlie w jednym ruchu jest w stanie tak umieścić kółka, by pozostały tylko dwa pola nie leżące w jednym rzędzie i kolumnie. To jak wszyscy wiedzą daje wygraną w następnym posunięciu. W pozostałych czterech sytuacjach Charlie umieszcza kółka tak, że pozostają cztery wolne pola, z których dwa leżą w jednym rzędzie (lub kolumnie), a pozostałe dwa również w jednym, ale innym rzędzie (lub kolumnie). Ta sytuacja z kolei logicznie przypomina tę opisaną przez wszystkich po pierwszym ruchu Charliego „b-e-h” i taka sama jest też metoda doprowadzenia do zwycięskiego dla Charliego finału.
Nie rozpisywałem wszystkich wariantów, gdyż strategia nie jest skomplikowana i zainteresowani, myślę, sami sobie z tym poradzą.
Pozdrawiam
AB
Ha! To musi być gra Batman. Jest miasto o takiej nazwie w Turcji 🙂 i odległość się zgadza.
Ujawniam „strzał”, bo to nie Batman. Czy w ogóle jest dostępna polska wersja tej gry? (mp)
No ale Manila to już musowo poprawna odpowiedź.
Nawiasem mówiąc Byzantium (historyczna nazwa Isanbułu) też jest całkiem blisko, brakuje ~700km. No i Byzantium został wydany jakiś czas temu w Polsce.
A czy Batman został wydany w Polsce? Nie mam pojęcia, podejrzewam, że nie. Poza tym na boardgamegeeku to dużo tych Batmanów różnych jest, no i chyba to nie jest za bardzo fascynująca planszówka.
Pierwsza zagadka – taka sytuacja nie mogła nastąpić przy zachowaniu zasad gry ;]