Heksomino
Heksomino to figura utworzona z sześciu kwadratów, a w znaczeniu zbiorowym – komplet takich figur o różnych kształtach. Wszystkich jest 35.
W zasadzie pojęcie to należy do matematyki rekreacyjnej, ale wiąże się też z tematami „serio”. Na przykład, 11 heksomin (niebieskie na rysunku) jest siatkami sześcianu.
W zadaniu indukcyjnym zamieszczonym w poprzednim wpisie najistotniejsze było odkrycie reguły podziału na heksomina diagramu 9 x 10. Klucz do parcelacji stanowiły cyfry znajdujące się w kwadratach – zera i jedynki, zaś mały przykład z rozwiązaniem był kluczem do rozszyfrowania – dzięki indukcji (od szczegółu do ogółu) – zagadkowej reguły.
Podejrzewam, że cytowana opinia o „maksymalnej trudności” zadania zniechęciła do poszukiwań, a propozycje tych z Państwa, którzy mimo to odważnie próbowali, okazały się zbyt zakręcone. Tymczasem jako zwolennik maksymalnie prostych i zwięzłych, rzekłbym „parterowych” zasad, nie ośmieliłbym się zachęcać do odkrywania czegoś „piętrowego”.
Mam nadzieję, że kilka poniższych komentarzy-podpowiedzi pozwoli już bez trudu ustalić szukaną regułę i rozwiązać zadanie z poprzedniego wpisu.
Łatwo zauważyć, że podstawę stanowi jakaś metoda oznaczania cyframi kwadracików tworzących figury heksomina. Z rozwiązania przykładu trudno to wywnioskować (szczegóły umożliwiające indukcję są jakby niekompletne), ale stosowanie tej metody nie gwarantuje, że wszystkie heksomina da się oznaczyć tylko zerami i jedynkami. Na figurach, znajdujących się na rysunku powyżej w górnym rzędzie, pojawiłyby się się także dwójki, na niektórych trójki, a na pierwszym nawet czwórki – oczywiście, te 17 heksomin nie występuje w rozwiązaniu zadania z poprzedniego wpisu.
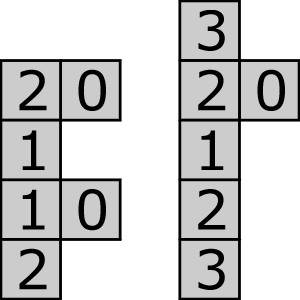
Czy te informacje wystarczą do ustalenia sposobu „numerowania” figur, a więc także do odkrycia reguły zadania? Jeśli jeszcze nie, to proponuję przyjrzeć się uważnie przykładowym oznaczeniom dwóch figur, wymagającym użycia dwójek i trójek:
A przed rozwiązaniem zadania z poprzedniego wpisu warto uporać się z prostszym podziałem diagramu trinarnego (w układzie są dwa heksomina z dwójkami).
W rozwiązaniu wystarczy podać, ile działek nie dotyka brzegu diagramu.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.



Komentarze
cyfra oznacza największa liczbe kratek w linii prostej jaka mozna przejsc na danym heksominie podazajac z tej kratki, z tym, ze liczenie zaczynamy od zera.
Moja propozycja na rozwiązanie sobotniego zadania to: 3 działki nie dotykają brzegu diagramu.
I jeszcze rozwiązanie dzisiejszej zagadki: 4 działki.
Teraz jasne:
cyfra w kratce oznacza najwiekszy odstep miedzy ta kratka a inna kratka w tej samej dzialce. Ale odstep liczony jest tylko poziomo lub pionowo i tylko w ramach dzialki, czyli bez przekraczania jej granic.
Rozwiazanie zadania trinarnego: 4 dzialki nie dotykaja brzegu.
a
Ja się włączam do gry:
w każdym polu stawiamy obserwatora – dalekowidza. Znajduje się on w pokoiku w kształcie heksomina. Widzi on te pola, które są w tej samej kolumnie/rzędzie i są odległe o co najmniej 2 pola (obserwator nie widzi przez ściany). i to by się zgadzało, gdyby w przykładzie z poprzedniego wpisu w lewym górnym rogu było:
2 0 1
0 0
1
Myślę dalej
Pozdrawiam
Michał
Albo inaczej:
Pole nie mówi ile pól z niego widać, tylko jak daleko jest najdalsze pole. Tak?
Pozdrawiam
Michał
To jest to!
mp
Drugą zasadę sformułowałabym tak:
Cyfra w kwadraciku wchodzącym w skład heksomina informuje jaki jest najdłuższy ciąg kratek stykających się bokiem (tworzących prostokąt) licząc od danego pola w jednym z możliwych kierunków, a konkretnie: ile kratek znajduje się między pierwszą a ostatnią w tym ciągu.
Oczywiście wszystko w obrębie heksomina.
Pozdrawiam
Magda
Trudno mi jakoś prościej zdefiniować tę regułę.
Biorąc od Michała propozycję obserwatora:
Liczba w polu jest o 1 mniejsza od maksymalnej liczby pól należących do danego heksomina, jakie „widać” w linii prostej.
Czyli np.: 0 musi należeć tylko do „dwupolowych linii” w heksominie.
1 musi być na początku co najmniej jednej „trzypolowej linii” i nie może być na początku „linii czteropolowej” (tam będzie 2).
Rozwiązanie nowego zadanie: 4 działki nie dotykają brzegu diagramu.
Rozwiązanie zadania z poprzedniego wpisu: 3 działki.
Graficznie:
http://pokazywarka.pl/48yv7n-2/