Binarnie indukcyjnie
Co to za zadanie diagramowe, w którym wiadomo, o co chodzi. Nie tylko napisano, co należy zrobić, ale zwykle jeszcze podany jest przykład. To zbyt wygodne i mało oryginalne. Domyślić się instrukcji na podstawie przykładu – to dopiero sztuka.
Po takim wstępie stali goście Łamiblogu już wiedzą, że będzie indukcyjnie. I po raz ostatni binarnie.
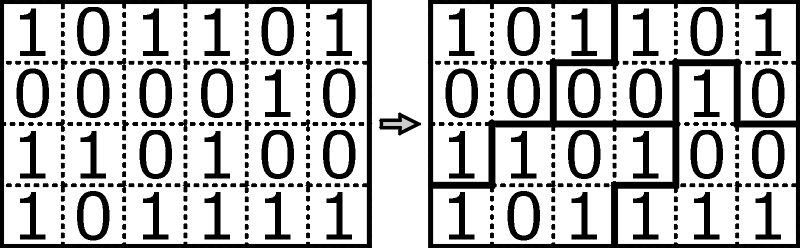
A zatem najpierw przykład w wersji mini oraz jego rozwiązanie:
Na podstawie rozwiązanego przykładu należy wyindukować, jakie są zasady zabawy, a następnie rozwiązać, zgodnie z tymi zasadami, poniższe zadanie:
Z przykładu łatwo się domyślić, że diagram należy podzielić na działki. Ale jakie jest kryterium podziału? – to kluczowe pytanie. A w ostatecznym rozrachunku wystarczy podać, ile działek nie sięga brzegu diagramu. Oczywiście, wystarczy także opisać tajemniczą działkową zasadę.
Moi łamiblogowi konsultanci stwierdzili zgodnym chórem (chór był tym razem dwuosobowy), że rozszyfrowanie zasady jest „maksymalnie trudne” i poddali się. Czy mieli rację?
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.


Komentarze
Według mnie, zasady w przykładzie są takie:
– prostokąt dzielimy tyle działek, ile wynosi szerokość prostokąta (4)
– liczba kratek w każdej działce wynosi tyle, ile długość prostokąta (6)
– jeśli w działce zsumujemy wszystkie liczby ustawione w pionie, to te sumy tworzą ciąg kolejnych liczb (4,5,6,7 )
101+00+1=110, 1+10+01+1=101, 0+10+0+10=100, 1+101+01=111.
Odpowiednio w zadaniu prostokąt trzeba podzielić na 9 działek po 10 kratek, zawierających sumy liczb: 9,10,11,12,13,14,15,16,17.
Ciekawe; ale oryginalne reguły (dwie) są znacznie prostsze. Podpowiem pierwszą, łatwą do odkrycia: wszystkie działki są, jak w przykładzie, 6-kratkowe.
mp
Reguły, wg których możliwe jest jednoznaczne zrobienie przykładu:
1. Prostokąt dzielimy na działki po 6 kratek każda.
2. Cyfra 1 w obrębie jednej działki musi sąsiadować z min. jednym ‚blokiem’ 01 lub 11 w prostej linii (tworząc ciąg 101 lub 111). W przypadku bloku 11 tylko pod warunkiem, gdy środkowa 1 spełnia warunek z 101 (lub 111 – i dalej rekurencyjnie).
Ale już dla dużego prostokąta rozwiązań jest sporo. Nawet gdyby dodać jakiś warunek typu „nie ma w działce ciągu 4-cyfrowego w prostej linii”. Jasne – działek wewnątrz będzie 3, ale ich właściciele będą się sądzić do końca świata.
Reguła (2) jest znacznie prostsza, co nie znaczy, że łatwa do znalezienia.
mp
Hmmm…. jak na razie podzielam zdanie konsultantów… ciężko jest złapać regułę, ale nie poddaję się, zostały jeszcze dwa dni:)
Moja propozycja drugiej reguły:
W podziale muszą wystąpić liczby najwyżej trzycyfrowe i dodatkowo „palindromiczne”, czyli 0,2,5 lub 7.
Rozwiązanie: trzy działki nie sięgają brzegu.
Dobrze więc, zasada 2:
Każda jedynka w bloku tworzy ciąg 101 lub 111 – i są to jedyne ciągi trzycyfrowe.
Ale zadanie nie podoba mi się z 2 powodów:
– nadto na mój gust sprawdza skorelowanie rozumowania rozwiązującego z układającym zadanie miast intuicyjności w rozwiązywaniu
– rozwiązanie (3 działki) pozostaje bez zmian ;].
(a jeśli i to jest źle to ja się poddaję)
update do zas. – „i nie ma ciągów większych”
Hmmm jesli dobrze rozpracowalem to to jest jedno z dwóch rozwiązań:
http://img714.imageshack.us/img714/2743/bini2.jpg
Kurcze, pomylilem sie w rozwiazaniu i nie chce mi sie drugi raz malowac, wiec napisze:
chodzi o to by ciag 101 lub 10101 byl w poziomie w jednej parceli, a w pionie ‚1’ nie moga byc obok siebie w jednej parceli.
choc to co napisalem rodzi dwa rozwiazania przykladowego rozwiazania 6×4
Następny wpis w środę, czyli jest jeszcze trochę czasu na indukowanie.
Zagadkowa reguła jest mniej zakręcona, niż proponowane dotychczas. Podpowiem, że nie ma nic wspólnego z układem dwójkowym poza skojarzeniem formalnym (zera i jedynki).
m
Hmmm, a może każdy poziom parceli musi mieć na początku i na końcu ten sam symbol (zero lub jedynkę), czyli jeśli dane ‚pietro’ konkretnej ‚parceli’ ma z lewej strony ‚0’ to musi mieć je też z prawej. Dotyczy to każdego piętra: co po lewej to po prawej, oczywiście pojedyncze pole, może byc dowolnie: zerem lub jedynką.
Teraz sprawdzę tą regułę, którą zostałem nagle olśniony, mam nadzieje, że to było prawdziwe olśnienie 🙂
Powiedziałbym, że to jest lekkie ciepełko:)
mp
Zapomniałem dodać, że to piętro ma byc ‚palindromem’. Pisałem i pisałem a miałem jeden wyraz na myśli: palindrom!
na obu końcach każdego trimina w kształcie litery I, które jest częścią 6 polowej działki – musi być 1
pozdr
Tak, ale tylko wtedy, gdy jest „binarnie”.
mp
PS poniewczasie zauważyłem, że komentarz jest pod tym wpisem, a moja odpowiedź uwzględnia następny wpis. Gdyby następny wpis pominąć, to komentarz jest bardzo trafny, a podana reguła bardziej zwięzła i prosta niż moja. Gratuluję!