Numerowanie mostów

Hashiwokakero, a krótko hashi, czyli mosty, to łamigłówka przedsudokowa, czyli współczesna klasyka. Debiutowała w Japonii w roku 1990 i dziś jest w tym kraju na emeryturze, czyli w druku pojawia się rzadko na zasadzie wspominka. Przypomnę więc, że polega na łączeniu liczb jednopasmowymi (jedna kreska) i dwupasmowymi (dwie kreski) mostami. Z każdej liczby może wychodzić w sumie dokładnie tyle pasm, jak jest jej wartość. Mosty nie mogą się przecinać, a powstały liczbowo-mostowy układ powinien tworzyć jedną spójną całość. Gwoli jasności mini przykład:

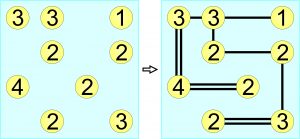
Przypomnienie łamigłówki hashi jest wstępem do jej „odwrotności”.
Na diagramie mosty są oznaczone, a do kółek należy wpisać liczby zgodnie z zasadą, która… nie jest podana. Jest to więc łamigłówka indukcyjna, czyli instrukcję obsługi trzeba samemu rozszyfrować na podstawie poniższego przykładu, co nie powinno być trudne:

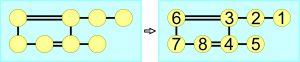
A potem rozwiązać zadanie:

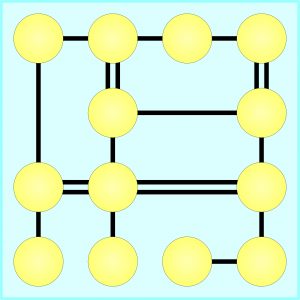
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze

[Adaś]

Zdaje się, że primo, numerujemy od 1 do pechowo, secundo, linia pojedyncza oznacza różnicę o jeden, podwójna linia to różnica większa od jeden. Podążając, lewy dolny róg może trzymać 1, w górę 2, 3, w prawo 4, 5, 6. Na dole, druga z lewej, bez styku z 1, może być 13, do góry 12, 11. Z 11 w prawo 10, z 10 w dół 9, 8, z 8 w lewo 7 (znowuż dolna linia). Finalmente, z 9 mamy podwójną linię w lewo do 12, a z 10 także podwójną linię do góry, do 6.

Powinienem uwolnić zawczasu, ale byłaby to podpowiedź, bo jest trochę dobrze i trochę źle. Więc nie uwalniam.
mp

[aps1968]

Zasada jest taka, że most pojedynczy oddziela liczby kolejne, a liczby, z których jedna jest dwukrotnością drugiej – podwójny, przy czym nie musi to być dla wszystkich par, w przykładzie nie są połączone 2=4 ani 5-6. Podejrzewam, że między 1 i 2 można dowolnie. Liczby od 1 do n nie mogą się powtarzać, więc w zadaniu należy rozmieścić liczby od 1 do 13.
Wychodząc od 1 na 3. polu od lewej w dolnym rzędzie, mamy w prawo 2, w górę 3, dalej w lewo 6, i dalej w lewo 12, a w dół 13. Od 3 w górę 4, dalej w lewo 5, w górę od 5 10 i w górę od 4 8, między 10 i 8 9. W lewo od 10 11, połączone z 12. Pozostaje 7 – w dół od 6. Kolejno rzędami mamy zatem:
11 10 9 8
x 5 x 4
12 6 x 3
13 7 1 2
Jeśli szukając innego rozwiązania damy 1 na miejsce 13, to w górę mogłoby być 2, dalej w prawo 4, a w górę 3, i od 3 w prawo znów 4, a więc sprzeczność. Jeszcze łatwiej widać sprzeczność, gdy 1 umieścimy na miejscu 7, w górę 2, i po bokach musiałoby być dwa razy po 4. No a 1 może być wyłącznie na polu, połączonym z jednym tylko innym polem.

[OlaGM]

Pojedyncza kreska oznacza +1, a podwójna oznacza x2.
11 10 9 8
5 4
12 6 3
13 7 1 2

[apartado]

Wierszami od góry:
11,10,9,8
5,4
12,6,3
13,7,1,2

[ersonasolidna]

11-letnia córka znalazła regułę w kilka sekund:
– pojedyncza kreska oznacza różnicę o 1
– podwójna kreska oznacza iloczyn/iloraz 2 pomiędzy połączonymi liczbami
– liczby występują po kolei od 1 i nie mogą się powtarzać

Rozwiązanie (nie wiem, czy jedyne):

11 10  9  8
    5     4
12  6     3
13  7  1  2

[Brzeszczot1978]

Zakładam, że reguła jest następująca:
– jednopasmowy most łączy liczby, których róznica wynosi dokładnie 1
– dwupasmowy most łączy liczby, z których jedna jest dwukrotnością drugiej

Rozwiązanie:

11, 10, 9, 8
5, 4
12, 6, 3
13, 7, 1, 2

[endywia]

Jedna kreska – różnica 1 między liczbami.
Dwie kreski – jedna liczba 2 razy większa/mniejsza od drugiej.
11-10-9-8
5 4
12=6 = 3
13 -7 – 1-2

[Spytko z Melsztyna]

Można usunąć trzy mosty. W programie nie korzystałem z połączeń między 12=6=3 oraz 5-4.