Zero-jedynkowo
Amerykanie się w tym roku nie popisali. Zadania zamieszczane w ich mistrzostwach dla główkołamaczy zawsze uważałem za niemal wzorcowe. Tegoroczne, jako całość, nie potwierdzają tej opinii. Wymagają raczej dłubaniny, spostrzegawczości i kombinowania niż główkowania, a nowych ciekawych pomysłów jest jak na lekarstwo (dla większości interesującą nowość stanowi zapewne tylko sukoro). To, że znaczna część zadań nie trzyma dotychczasowego topowego poziomu nie znaczy, że nie mogą się podobać. Przeciwnie, atrakcyjnością mimo wszystko górują nad zamieszczanymi w wielu innych turniejach (wspomniane sukoro jest rodzynkiem z najwyższej półki), więc jeśli ktoś ich nie zna, a lubi intelektualny relaks, tego zachęcam do zajrzenia na stronę mistrzostw, gdzie nadal są dostępne (po zalogowaniu się).
Jest wśród tych zadań synteza krzyżówki liczbowej (Criss Cross) z podpowiedziami, wymagająca szczypty myślenia i dłubaniny wspartej furą spostrzegawczości. Charakterystyczne, że liczby są binarne, czyli złożone z zer i jedynek. Gdy rozwiązywałem to zadanie, zaświtało mi, że binarne krzyżówki już kiedyś w amerykańskich mistrzostwach były. Sprawdziłem i okazało się, że istotnie – dokładnie 10 lat temu, ale znacznie bardziej zakręcone. Prezentowałem już kiedyś takie zadania. Przypomnę jeszcze jedno jako wstęp do ogólniejszego zagadnienia.
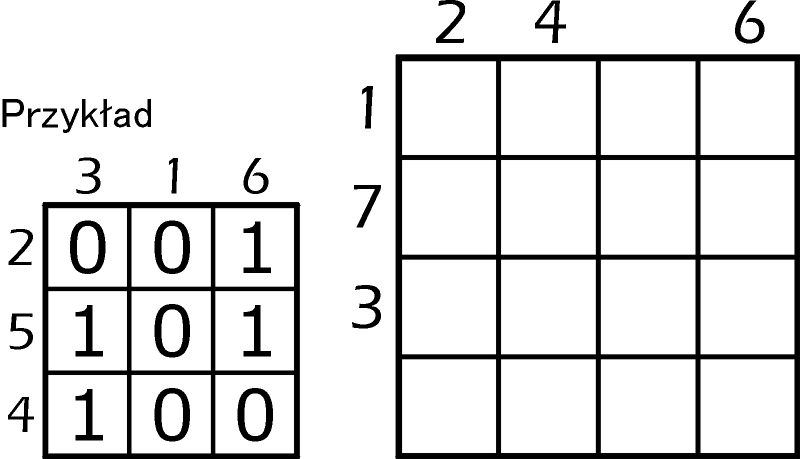
Po wpisaniu zer i jedynek do pól diagramu 4×4 w czterech rzędach i czterech kolumnach pojawi się osiem liczb binarnych. Cyfry należy wpisać tak, aby kolejność liczb binarnych (od najmniejszej do największej) była zgodna z oznaczoną obok diagramu – przed rzędami i nad kolumnami.
Piszemy o tym, co ważne i ciekawe
Teraz będziesz ważką
Rozmowa z dr Katarzyną Żak-Jasińską, pediatrą zajmującą się opieką paliatywną, o przeżywaniu ostatnich chwil z dziećmi i szukaniu drogi powrotu do życia po ich stracie.
A teraz ogólniejszy problem.
Czy do pól diagramu 4×4 można wpisać zera i jedynki tak, aby
– w trzech kolejnych polach (w rzędzie, kolumnie lub na przekątnej) nigdzie nie występowały trzy jednakowe cyfry;
– w czterech rzędach, czterech kolumnach i na dwu przekątnych pojawiło się dziesięć różnych liczb binarnych?
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.

Komentarze
Zad.1.
Można. Np. tak:
1010
0011
1100
0101
1 zadanie:
0011
1101
0110
1110
10 zadanie:
Jeśli dobrze zrozumiałem chodzi o remis w grzy kółko i krzyżyk na planczy 4×4.
Przykład, że da się to zrobić:
0110
1001
0110
1001
11 zadanie:
1111
0100
0101
0011
0011
1101
0110
1110
Dlaczego przy diagramie po prawej nie ma liczby 5?
Poszła sobie bo nie była niezbędna :).
mp
Zadanie z diagramem
0011
1101
0110
1110
1: http://pastebin.com/7fBsAbdU
2: http://pastebin.com/y0KiSrBz
3: http://pastebin.com/6kYzrctG
Pierwsze
0011
1101
0110
1110
Drugie np.
0011
0101
1010
1100
Trzecie np.
0110
1110
1000
1010
Nie ma zadania trzeciego. Dwa warunki dotyczą tego samego drugiego zadania (problemu). Układ liczb binarnych powinien spełniać oba podane warunki równocześnie.
mp
Obydwa warunki spełniają liczby:
0101
0100
1011
1100
Teraz dopiero dotarło do mnie o co chodzi w tym zadaniu.
Nie da się rozegrać partii w „zero-jedynkę”, aby zakończyła się remisem (żaden z graczy nie uzyskał trzech swoich znaków pod rząd) i dodatkowo powstałe liczby we wszystkich 10 kierunkach były różne.
Nie wiem jeszcze tylko jak to zgrabnie udowodnić
Musimy w diagramie rozmieścić 10 liczb binarnych, a mamy konkretne 10 do dyspozycji. Da się to wykonać na 4 sposoby:
0011
1101
0010
1010
0101
0100
1011
1100
I analogiczne (zamienione 0 1)
1010
1011
0100
0011
1100
0010
1101
0101
Żadne nie spełnia warunków zadania.
Wygląda na to, że zadanie ogólne nie ma rozwiązań nawet bez liczb na przekątnych
fenix86: można udowodnić poprzez sprawdzenie każdej możliwości. Mniej więcej tak dowodzono rozwiązywalność w 20 ruchach kostki Rubika. Tyle, że tu jest absurdalnie mało możliwości.
Rozwiazanie problemu ogolnego: mozna!
1100
0010
1101
0101
a
Zadanie 1
0011
1101
0110
1110
Zadanie 2
0011
1101
0010
1010
1100
0010
0100
0011
1010
1011
0100
0011
0101
0100
1011
1100
I to tyle.
bd, udowodniłem to najpierw na komputerze, ale właśnie pisząc zgrabne rozwiązanie, miałem na myśli takie bez jego użycia. Da się to zrobić, rozważając główne 2 przypadki, które rozpadają się na kilka pomniejszych. Opis byłby dość obszerny dlatego zrezygnowałem z umieszczania go tutaj.
Ostatecznie nie wiem czy te cztery wyniki jakie dało się uzyskać zadowalają naszego gospodarza, czy nie.
Gospodarz jest usatysfakcjonowany czterema wynikami podanymi przez antypa.
m