Bez polityki

15 kwietnia 2023
Marek Penszko

Kryptarytmetycznie kusząca sytuacja: wyrazy KACZYŃSKI i TUSK składają się w sumie z dziesięciu różnych liter. Trudno się oprzeć ryzykownemu mnożeniu:
TUSK × x= KACZYŃSKI
I równie trudno uciec od skojarzeń i podtekstów politycznych. Z jednej strony „współdziałanie” obu słów sugeruje pojednanie. Z drugiej jednak drzemiąca w nas skłonność do antagonizmów może rodzić pytania w rodzaju: jaką wartością jest KACZYŃSKI, jeśli TUSK jest pierwszy (także jako liczba pierwsza)? Albo (co gorsza): ile TUSK-ów potrzeba, by zrównoważyć KACZYŃSKI-ego?
Oba te pytania poniekąd dotyczą poniższego zapisu mnożenia, ale mimo to namawiam do wzięcia tego „na miękko”, czyli porzucenia aspektu politycznego i skupienia się na matematyczno-logicznym.

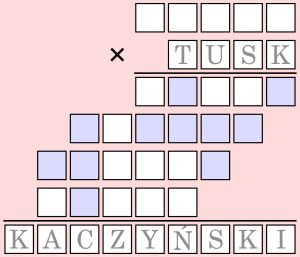
Jak zwykle w kryptarytmach chodzi o rekonstrukcję działania, czyli ustalenie, jakie cyfry powinny odpowiadać literom, a liczby wyrazom, aby mnożenie było poprawne. Za jednakowymi literami ukrywają się oczywiście takie same cyfry, a za różnymi – różne.
Kluczem do rozwiązania są NIEbieskoszare kratki w iloczynach cząstkowych – wszystkie, w których powinny się znaleźć cyfry NIEparzyste (w kratkach z mnożną, mnożnikiem i iloczynem cyfr nieparzystych nie oznaczono). Ponadto istotne jest dodatkowe działanie pomocnicze:
TU+SK=100.
Wprawdzie TUSK, jak wspomniałem wyżej, jest liczbą pierwszą, ale informacja ta nie wydaje się niezbędna do rozszyfrowania mnożenia.
Kryptarytm mimo pokaźnych rozmiarów wygląda na rozwiązywalny bez większego trudu na piechotę, czyli korzystanie z programu komputerowego można sobie darować. Ewentualnie może się przydać małe wsparcie kalkulatorowe. Natomiast niektórzy programiści zapewne nie omieszkają sprawdzić, ile rozwiązań ma podane na wstępie mnożenie ogólne.

Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.