Krzyżowanie bliźniaków

16 lipca 2022
Marek Penszko

Postanowiłem nawiązać do poprzedniego wpisu, a pretekstem do tego jest osobliwa dyskusja, która wywiązała się w komentarzach. Przypomnę: zadanie polegało na podaniu dowodu, że jeśli pomnożymy liczby tworzące dowolną parę liczb pierwszych bliźniaczych, a następnie dodamy cyfry otrzymanego iloczynu i ewentualnie cyfry powstałej i każdej następnej sumy – aż do otrzymania jednocyfrowego wyniku (tzw. osc, czyli ostatecznej sumy cyfr) – to osc zawsze będzie równe osiem.
Elementarna wersja dowodu zaczyna się od zauważenia, że z trzech kolejnych liczb naturalnych przynajmniej jedna musi być podzielna przez 2 i dokładnie jedna przez 3. Jeśli z tych trzech liczb pierwsza i trzecia są liczbami pierwszymi (bliźniaczymi) – a więc niepodzielnymi ani przez 2, ani przez 3 – to podzielna przez 2 i przez 3, czyli przez 6, musi być liczba środkowa. Zatem pierwsza z liczb bliźniaczych wyraża się wzorem 6n-1, a druga 6n+1, zaś iloczyn liczb bliźniaczych to 36n2-1; 36n2 jest podzielne przez 9, czyli suma cyfr tej liczby równa jest 9, a po odjęciu 1 zostaje 8.
Ku nie tylko mojemu zdziwieniu Mauro Rossi z góry zanegował dowód – nie podając go i uznając za hipotezę, co uzasadniał hipotezą liczb pierwszych bliźniaczych, o których nie wiadomo, czy tworzą ciąg skończony, czy nie. Mam nadzieję, że adwersarz zmienił zdanie, choć warto dodać, że w sieci można znaleźć informację świadczącą na jego korzyść – towarzyszy ona ciągowi A136050 w Encyklopedii ciągów (OEIS). Proszę zwrócić uwagę na podane tam „Conjecture”, czyli hipotezę (przypuszczenie). Wytłumaczenie jest proste. Choć OEIS firmuje ceniony matematyk Neil Sloane, to zwykle bezpośrednio obsługują ją jego podopieczni i błędów w niej nie brakuje. W tym przypadku słowo „Conjecture” należałoby usunąć, bo poprzedza „True”.
Kończąc bliźniaczy temat proponuję ułożyć krzyżówkę 3×3 z sześciu 3-cyfrowych bliźniaków wybranych z 54 wszystkich 3-cyfrowych podanych obok diagramu.

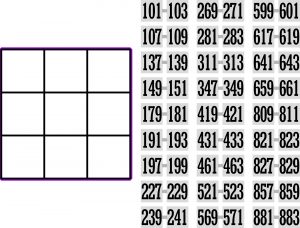
Analogiczna krzyżówka 2×2 jest tylko jedna (poziomo: 11, 73; pionowo: 17, 13). Ile jest „bliźniaczych” krzyżówek 3×3 – to zadanie dla komputerowców. Jedną można jednak utworzyć bez większego trudu i w znacznym stopniu na logikę.

Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.