Za kratki
W lipcu 2014 roku umieściłem Leszka Millera za kratkami. Efekt tego incydentu miał się znaleźć w dodatku „Co jest grane” do Gazety Wyborczej jako przykład do zadania stanowiącego zajawkę kolejnego numeru ówczesnego dodatku dla główkołamaczy – „Na pamięć”. Tekst zaczynał się wybitą wersalikami mocną informacją: …LESZEK MILLER ZA KRATKAMI! Dalej było łagodniej, jaśniej, konkretniej, a za kratkami pojawili się także inni politycy. Cytuję:
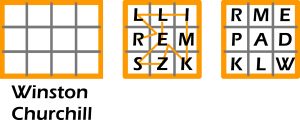
WINSTONA CHURCHILLA można sprytnie wsadzić za kratki… Chodzi o to, aby w kratki diagramu 4×3 wpisać w pewien szczególny sposób 12 liter, tworzących imię i nazwisko tego polityka – 10 różnych (C, H, I, N, O, R, S, T, U,W) oraz dwie litery L. Należy to zrobić tak, aby, zaczynając od W i przechodząc z kratki do kratki –wprost lub na ukos (przez róg) –wyznaczyć trasę, na której kolejne litery utworzą imię i nazwisko WINSTON CHURCHILL. Gwoli jasności za kratki trafił LESZEK MILLER (pierwszy diagram 3×3) – także w tym przypadku dwie litery L są kolejnymi w nazwisku, więc obie znajdują się w diagramie; gdyby kolejnymi nie były, wystarczyłoby jedno L, jak w przykładzie na drugim diagramie 3×3, gdzie za kratkami figuruje inny nasz polityk. Który?
Temat był rozrywkowo-umysłowy i potraktowany z przymrużeniem oka, ale w ostatniej chwili uznano, że stanowi jednak przegięcie i tekst się nie ukazał.
Wspominam o tym, ponieważ nadarza się okazja, aby rodzaj i charakter zadania (zwykle zwanego królówką, bo linia odczytu jest jakby trasą króla szachowego) potraktować nieco poważniej. Pojawiło się bowiem przynajmniej kilku polityków, którzy bez wątpienia powinni trafić za kratki nie tylko łamigłówkowo, a którzy literowo się do tego nadają. Właśnie pod względem literowym pasuje niejaki SIERGIEJ ŁAWROW. Proponuję zatem ulokować go za kratkami. Wielkość diagramu-więzienia jest wiadoma – 10 kratek, bo tyle jest różnych liter. Natomiast kształt diagramu musi spełniać dwa warunki:
– powinien być symetryczny (przynajmniej jedna oś symetrii);
– obwód diagramu powinien być możliwie największy (jednostka – bok kratki).
Praktycznie rozwiązaniem jest więc kształt tiurmy dla ministra, a dopiero w drugiej kolejności sposób, w jaki trafia on za kratki.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Dwa rozwiązania z osią symetrii:
SIE
GRŁJ
OWA
AWSG
ŁORI
_JE_
„Więzienie” środkowosymetryczne
_OW
GRA
EIŁ
SJ_
Obwód 14.
To jako „przygrywka”, bo obwód przymały.
mp
Widzę, że razem z „innym naszym politykiem” za kratki dostał się też PAD.
Przypadek…?
Idea zadania jest bardzo podobna do gry Boggle, w której celem jest znalezienie jak najwięcej wyrazów w „diagramie” 4×4, powstałym z rzutu 16 kostkami , na ściankach których umieszczone zostały litery.
Diagramy bywają różne, zwłaszcza w Rosji:
obwód=22
Obszar tiurmy powinien być spójny (stykanie się tylko rogiem wyklucza spójność).
mp
Obwód 24:
[ ] S [ ] [ ] [ ] A [ ]
G I E J Ł O W
[ ] R [ ] [ ] [ ] R [ ]
Zakładam warunek „spójności obszaru” tj. komórki muszą się łączyć krawędziami, wierzchołkiem nie wystarczy. Bez tego można by np. wysunąć J w pionie zwiększając brzeg o 2 itp.
Liter powinno być 10 (11 byłoby tylko wtedy, gdyby w imieniu lub nazwisku występowała geminata).
mp
Jeżeli diagram może mieć dziurę, to mam taką 20’kę:
lub bez dziur z ukośną osią symetrii (również 20):
Dziura odpada, ale ukośna symetria z obwodem 20 to miom zdaniem max.
mp
Oczywistość, błąd i nieuwaga. Lepsza próba L=20:
S
G I E J
R Ł
O W A
Słabe te wklejanie:
https://naforum.zapodaj.net/aaabd01f742c.jpg.html
Poproszę wielokąt spójny, czyli bez dziury.
mp
Wszystkie poniższe układy mają długość boku równą 18.
symetria pionowa:
J..S
ŁEIG
.AR.
.OW.
symetria pionowa (inny układ liter):
S..O
IGRW
.EA.
.JŁ.
symetria pozioma:
..S.
.JI.
ŁAEG
.WR.
..O.
symetria obrotowa:
..A.
.OWŁ
.RJ.
SGE.
.I..
W takim samym kształcie jak @xswedc litery rozmieszczam inaczej – czyli inne rozwiązanie.
Problem polega na tym, że obwód diagramu wychodzi mi 16.
. Ł J .
. E A O
S I R W
. G..
W sumie nie widzę tu poprawnego rozwiązania z ukośną symetrią i obwodem 20, rozwiązanie xswedc ma obwód 16…
Ale coś takiego powinno być ok:
S
GI
xRE
xOWJ
xxxAŁ
Tak, to jest OK (u xswedca istotnie obwód = 16)
mp
Ten wielokąt z dziurą jest jak najbardziej spójny (jego wnętrze jest jednym kawałkiem) o ile tylko styka się krawędziami a nie wierzchołkami. Ma też oś symetrii więc spełnia warunki zadania. Nie jest natomiast jednospójny (jego brzeg nie jest jednym kawałkiem), ale takiego wymogu nie sformułowano.
Specjalnie szukałem takiego kształtu, który w zadanych ramach nie tylko zmaksymalizuje długość brzegu, ale też zapewni osadzonemu maksymalny dyskomfort 😉
Zgadza się. Nie uwzględniłem różnicy między spójnością a jednospójnością.
mp
To jest prawdziwa dwudziestka:
Nie wiem jednak, jak zakwalifikować spójność. Mimo okienka – brzeg można obrysować bez oderwania ołówka.
Moim zdaniem jest dziura i jednospójne nie jest. A co na to Markoniusz?
mp
Moje podejście jest rekreacyjne, więc figura jest dla mnie spójna jeśli można odwiedzić wszystkie jej pola, poruszając się jak wieża szachowa.
@ xswedec
O ile pamiętam jest jednospójny bo każde dwa punkty tego obszaru możemy połączyć łamaną zawartą w tym obszarze (ale nie odcinkiem więc nie jest wypukły, co jest oczywiste).
Prościej byłoby dodać do zadania wymóg, że kratki muszą się łączyć całymi krawędziami.
Zaproponowany wymóg nie wyklucza dziury. Najprostszy byłby wymóg „precz z dziurą”:)
mp
PS. Chodzi o to, żeby wnętrze było jednym kawałkiem. Gdyby np. z układu xswedca usunąć ‚E’ to ten obszar utraciłby spójność bo tylko jego domknięcie trzyma się w kawałku tylko dzięki 2 punktom brzegu.
Tak jak w poniższym przypadku (o ile mi wyjdzie):
XX X X XX@Markoniusz, @mp
Przy takich zadaniach oprócz warunków geometrycznych warto też spojrzeć na linię tekstu. W moim diagramie
konieczne jest przejście od A do W, czyli przez ten nieszczęsny narożnik, którego kratki są rozdzielone linią obrysowującą.
Logiczne by było – skoro diagram jest spójny – aby droga poprzez litery odbywała się również w ramach tej spójności, a nie przeciw niej. To oczywiście jest dyskusyjne i zależne od autora zadania, ale ponieważ mnie trochę drażni takie skakanie przez płot, to zwracam na to uwagę. Gdyby nie ten drobiazg, to zażarcie walczyłbym o uznanie poprawności rozwiązania.