LC-rama
Literama jest z natury zadaniem średnio trudnym. Oznacza to, że zależnie od rodzaju i rozmieszczenia kluczowych liter przy brzegu diagramu droga do rozwiązania może być mniej lub bardziej kręta, ale zadanie jako propozycja zabawy zawsze ma sens. W przypadku łamigłówek z natury trudnych próby ich zmiękczenia wiodą na manowce trywialne, czyli bezsensowne.
Gwoli ilustracji przykład prostej literamy, którą rozwiązuje się, jak mawia znajoma matematyczka, o tak: pyk, pyk, pyk.
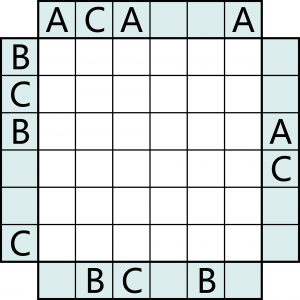
Info dla nowicjuszy:
W niektóre kratki należy wpisać litery A, B, C tak, aby w każdym rzędzie (wierszu i kolumnie) występowały trzy różne litery – każda dokładnie raz. Pól w rzędach jest sześć zatem trzy kratki w każdym rzędzie pozostaną puste. Kluczem do rozwiązania są litery-podpowiedzi przy brzegu. Każda jest taka sama, jak najbliższa litera w rzędzie, na przedłużeniu którego znajduje się podpowiedź.
Literamę można uznać za niepełny lub częściowy kwadrat łaciński, czyli taki, w którym w każdym rzędzie pominięto taką samą liczbę pól. Albo inaczej: w polach tych znajduje się dodatkowa identyczna litera, np. X.
Z wielu prób uczynienia z literamy zadania z natury trudnego na uwagę zasługuje zmiana jej w LC-ramę, czyli LiteroCyfroramę. Zmiana sprowadza się do zastąpienia X-a zbiorem cyfr, czyli w przypadku literamy ABC 6×6 cyframi [1,2,3].
Ogólna instrukcja obsługi zmienia się nieznacznie: w każdym rzędzie powinny pojawić się trzy litery (A, B, C) i trzy cyfry (1, 2, 3), więc nie ma pustych pól. Podpowiedź przy brzegu działa tak samo, tylko może być literą lub cyfrą. Oczywiście podanie litery nie oznacza, że przed nią nie ma cyfr – i odwrotnie. Proszę sprawdzić, rozwiązując poniższe zadanie, że tym razem to nie przelewki – mimo pełnej informacji brzegowej – a na pewno nie pyk, pyk, pyk.
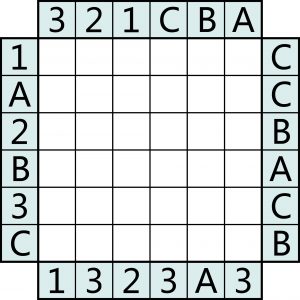
W rozwiązaniu wystarczy podać jakie cyfry i litery występują na przekątnych diagramu.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Pierwsza przekątna: A,A,1,B,1,B
Druga przekątna: 1,3,3,A,2,2
Zadanie z podanymi warunkami nie ma rozwiązania. Wystarczy sprawdzić ostatnią kolumnę. W niej litery można umieścić tylko w kolejności ABC a zgodnie z informacją w ostatnim wierszu C jest w nim pierwsze.
Zadanie pierwsze:
xxxBCA
xCAxxB
xxBCAx
AxxxBC
BACxxx
CBxAxx
Zadanie jest typu pyk, pyk, pyk bo cierpi na nadmiar informacji.
Górny wiersz
AxxxxA
Dolny wiersz
xBCxxx
Lewa kolumna
BCBxxx
Prawa kolumna
xxxCxx.
Wtedy dalej nie jest bardzo trudno ale nie pyk….
AA1B1B
133A22
AA1B1B
22A331
Ten poprzedni mój komentarz powstał w chwili „pomroczności jasnej”. Zadanie ma oczywiście rozwiązanie:
ABC132
3ABC21
C21AB3
213BCA
B3A21C
1C23AB
Przekątne:
AA1B1B
133A22
A użytkownikowi za naprowadzanie złą odpowiedzią należy się…
Dopiero po wykonaniu zobaczyłem, że omyłkowo jedną literę B zmieniłem na 3 przy przepisywaniu, ale i tak wyszło, co miało wyjść (tylko zmiana jednej literki B na 3 skutkowałaby błędem). Podobnie C i 1
\ AA1B1B
/ 22A331
Od góry:
AA1B1B
22A331
Jak słusznie zauważył Antyp1958, najlepiej zacząć od ostatniej kolumny. Od razu widać, że litery muszą być na dole, więc cyfry na górze. Kolejność w obu podzbiorach jest oczywista.
Następnie można wpisać wszystkie cyfry i literę C w pierwszym wierszu (zostają wolne dwie pierwsze kratki). Potem 3 na drugiej pozycji w pierwszej kolumnie itd. może nie pyk, pyk, pyk ale bez specjalnych problemów.
Na przekątnych nie występuje C.
AA1B1B; 22A331
ODP: AA1B1B, 22A331
ABC132
3ABC21
C21AB3
213BCA
B3A21C
1C23AB
Bardzo odprężające zadanie…
Jedna przekątna: AA1B1B
Druga: 133A22
W sumie niezbyt trudne.
Pozdrawiam,
Zacząłem od zadania właściwego:
abc132
3abc21
c21ab3
213bca
b3a21c
1c23ab
A potem wziąłem się za wstępne, to niby łatwiejsze:
xxxbca
xcaxxb
xxbcax
axxxbc
bacxxx
cbxaxx
Stopień trudności uznałem o dziwo za podobny. Zadania jako kategoria – przyjemne.
A, A, 1, B, 1, B
Druga przekątna: 1, 3, 3, A, 2, 2
AA1B1B
133A22