T-mina inaczej
Zadanie przed tygodniem polegało na podzieleniu diagramu obejmującego n^2 kwadratów (n×n) na tetromina (figury złożone z czterech kwadratów). Kluczem do tego były umieszczone w diagramie cyfry – każda znajdowała się w kwadracie jakiegoś tetromina i oznaczała, z iloma kwadratami tego tetromina sąsiaduje kwadrat z tą cyfrą. Przykład dla n=4 wyglądał tak:
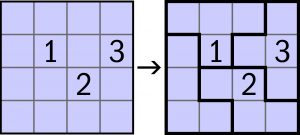
Tym razem cel jest taki sam, ale droga do celu, a więc znaczenie cyfr – trochę inne. Jakie? – to należy wywnioskować samodzielnie z przykładu:
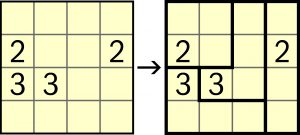
Jest to zatem kolejna zagadka indukcyjna, czyli analizując przykład trzeba rozszyfrować instrukcję obsługi, a następnie, korzystając z niej, rozwiązać nieco większe (6×6) zadanie:
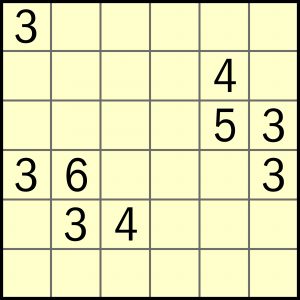
Bez warunku dodatkowego zadanie ma przynajmniej kilka rozwiązań. Chodzi natomiast o znalezienie takiego rozwiązania, w którym liczba kwadratowych tetromin (2×2) będzie jak największa. W rozwiązaniu wystarczy podać liczbę tetromin w kształcie litery T.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
W rozwiązaniu są dwa tetromina w kształcie litery T.
Panie Marku,
Oba moje rozwiązania: zarówno z trzema jak i z dwoma kwadratowymi tetraminami zawierają 2 tetromina w kształcie T.
Ale są też rozwiązania z dwoma kwadratowymi tetrominami i większą niż 2 liczbą T-tetromin
mp
Cyfra w tetrominie oznacza z iloma innymi tetrominami ono sąsiaduje. Gdy kwadratowe (2×2) są trzy, to w kształcie litery T są dwa.
Instrukcja obsługi:
każda cyfra ujawniona w diagramie należy do innego tetromina i informuje z iloma innymi tetrominami styka się ono bokiem (lub częścią boku).
Przy takiej instrukcji znalazłam rozwiązanie, w którym:
– są 3 kwadratowe tetromina,
– są 2 tetromina w kształcie litery T (w 4 i 5 kolumnie).
Rozważałam również stykanie się wierzchołkami oraz dwie ujawnione cyfry należące do tego samego tetromina, ale nie wymyśliłam niczego sensownego.
Zakładam, że cyfra (dokładnie jedna na kamień) oznacza ilość sąsiadujących (bokami) kamieni. Wtedy, z bodajże 17 rozwiązań, tylko jedno zawiera 3 kwadratowe kamienie (ich cyfry to 6 z czwartego oraz 3 i 4 z piątego rzędu planszy).
Ilu mamy T-akich sąsiadów? Zero.
Jednak jeżeli odpowiedź: „ilość T” jest jednoznaczna, to najlepsze z rozwiązań (5), które napotkałem – nie jest właściwym. Każde z nich zawiera różną ilość kwadratów 2×2 a jednocześnie część z nich nie zawiera „T”. A wtedy na nic wyróżnienie: Zero-Zero. Takiego symptomatycznego widoku, szkoda. Pięć kwadratów, 1-z szóstką, 2-z piątką, 3-z trójką, 4-z czwórką, 5-pusty.
Tak ale nie.
„Ale są też rozwiązania z dwoma kwadratowymi tetrominami i większą niż 2 liczbą T-tetromin – mp”.
Dwa kwadraty spojone w podłużny prostokąt, Parawanowiec zasłaniający cztery T-eki (T-3, T-3, T-4, T-5). Stąd już tylko kroczek do: ale jest też rozwiązanie z dwoma T-tetrominami i pięcioma kwadratowymi. Plus dwa warianty bez teki.
Najlepsze nie jest właściwym a ilość „T” nie jest jednoznaczna.
I co to ma wspólnego z gołębiami?
A kiedy przyleciały?
Szanowny Panie Marku, Szanowni Komentatorzy,
przepraszam.
Z poważaniem
uch ty