Jeszcze rok
Jakoś ciężko mi się rozstać z nowym rokiem, a ściślej – z przypisaną mu liczbą. Była w dwu poprzednich wpisach i poniżej pojawia się po raz trzeci, chyba ostatni. I chyba nie muszę wyjaśniać, o co w poniższej „wyliczance” chodzi. Jakiego konia należy dosiąść, każdy widzi. A główny problem polega na tym, ile jest sposobów dosiadu, czyli ile rozwiązań ma to szkieletowe dzielenie.
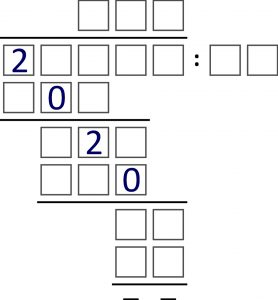
Jest jeszcze jeden problem – językowy. Ten sam bieżący rok jest w trzech kolejnych zadaniach. Czy w liczbie mnogiej mógłbym powiedzieć, że w tych zadaniach były trzy ROKI? Wątpliwość stąd, że jeśli są LATA, to oznaczają trzy RÓŻNE lata, a tu mamy przypadek szczególny: rok, rok i rok – i wszystkie jednakowe. Trudno wyobrazić sobie inną sytuację, w której grupę tworzyłoby kilka jednakowych lat. Może więc wyjątek, a właściwie odstępstwo od poprawności byłoby uzasadnione.

Komentarze
Aż się prosiło 😉
ROK*?=LATA
21280:40=532
21240:40=531
23240:40=581
23280:40=582
4 rozwiązania:
21240:40=531
23240:40=581
21280:40=532
23280:40-582
> Czy w liczbie mnogiej mógłbym powiedzieć, że w tych zadaniach były trzy ROKI?
A czemu chce Pan tak powiedzieć, skoro był jeden rok, a nie trzy? Sformułował Pan to precyzyjnie i zgodnie z prawdą: „Ten sam bieżący rok jest w trzech kolejnych zadaniach”. Liczba mnoga nie ma uzasadnienia, skoro prawda jest taka, że był tylko jeden rok, tyle że w trzech zadaniach – niczym jeden aktor odgrywający trzy role w trzech różnych filmach.
A tak poza tym, żartobliwie słowa „roki” zawsze Pan może używać 🙂
Na koniec polecam też hasło ze słownika etymologicznego Aleksandra Brücknera:
https://pl.wikisource.org/wiki/S%C5%82ownik_etymologiczny_j%C4%99zyka_polskiego/rok – odnotowano w nim dawną formę „roki”, która wyszła z użycia.
Ładnie wyjaśnione. Ale można kombinować, np. tak:
2020, 2020, 2020 – trzy jednakowe liczby oznaczające długość = trzy jednakowe długości = trzy długości.
2020, 2020, 2020 – trzy jednakowe liczby oznaczające rok = trzy jednakowe lata = trzy lata.
mp
Z góry przepraszam za offtopic, ale ośmielił mnie poruszony temat bieżącego roku, którego dotyczy także nurtująca mnie sprawa… więc jakiś związek z tematem jest. A tu jest jedyne forum jakie znam, władne ocenić czy ta sprawa jest godna uwagi z punktu widzenia matematyki rekreacyjnej.
Jak ktoś zauważył (https://wyborcza.pl/7,75400,25558194,2020-ten-rok-ma-w-sobie-matematyczna-zagadke.html) liczba 2020 jest tzw. liczbą autobiograficzną – jej pierwsza cyfra (tj. 2) wyraża ilość zer w zapisie pozycyjnym tej liczby, druga cyfra (0) – ilość jedynek, trzecia (2) – dwójek, czwarta (0) – trójek. Liczby autobiograficzne (w systemie dziesiętnym) są z definicji co najwyżej 10-cyfrowe; okazuje się że przy takich założeniach jest ich tylko siedem: 1210, 2020, 21200, 3211000, 42101000, 521001000, 6210001000.
Idea autodeskrypcji w odniesieniu do liczb wydała mi się b. ciekawa ale konsekwencje trochę rozczarowujące, na zasadzie – z dużej chmury mały deszcz. Czy nie ma tu już nic do zbadania? Przyszło mi do głowy, że ograniczenie długości liczby do 10 cyfr jest arbitralne, warunek autobiograficzności tego nie narzuca ani nie wymaga. Oczywiście, 10 cyfr wystarcza do opisywania liczby, ale mogą być kolejne cyfry, już nie opisujące i opisywane, a tylko opisywane.
Dokładniej, liczbę co najmniej 11-cyfrową nazwę AUTOBIOGRAFICZNĄ, jeśli:
– pierwsza cyfra wyraża liczebność zer (cyfr „0”) w zapisie dziesiętnym tej liczby;
– druga cyfra wyraża liczebność jedynek (cyfr „1”) w zapisie dziesiętnym tej liczby;
. . . . . .
– dziesiąta cyfra wyraża liczebność dziewiątek (cyfr „9”) w zapisie dziesiętnym tej liczby;
– każda następna cyfra została uwzględniona tj. zliczona przez jedną z dziesięciu pierwszych.
Wygląda na to, że zbiór liczb autobiograficznych jest w naturalny sposób znacznie większy niż się wydawało. Na szczęście skończony bo oczywiście liczba autobiograficzna nie może mieć więcej niż 90 cyfr. Tu uwaga techniczna, przy badaniu liczb autobiograficznych lepiej je traktować jako ciągi cyfr lub teksty, inaczej grozi nam szybko ‘stack overflow’.
Zatem spróbujmy coś jeszcze wycisnąć z tego tematu.
1) Znaleźć największą liczbę autobiograficzną. Jaka jest jej długość N*?
2) Znaleźć najmniejszą i największą liczbę autobiograficzną 11-cyfrową (N=11).
3) Czy dla każdego N: 11 ≤ N ≤ N* istnieje liczba autobiograficzna długości N?
45) Ile jest wszystkich liczb autobiograficznych? (nie mam pojęcia)
@Markoniusz
To z cyklu „Aż się prosiło”:
72100001000
… a potem to już mam z górki, bo tak:
821000001000
9210000001000
@apartado (11 stycznia o godz. 12:01 193831)
Biorąc pod uwagę ilość generowanej zabawy do zwięzłości sformułowania to zagadka bliska ideału. Efekt trochę psuje spora ilość rozwiązań, bo chyba jednak lubimy jednoznaczność.
Żeby ograniczyć ilość rozwiązań potraktowałem zmienną „?” jako literę różną od pozostałych (np. N lub X) a i tak znalazłem ich sporo (wątpię czy wszystkie) np:
207*8=1656
702*8=5616
409*8=3272
904*8=7232
418*5=2090
851*4=3404
416*5=2080
614*5=3070
345*6=2070
356*4=1424
643*9=5787
946*3=2838
452*8=3616
528*7=3696
952*4=3808
Jeśli „?” potraktować jako dowolną literę, niekoniecznie różną od pozostałych, to są jeszcze inne np.
308*8=2464
803*8=6424
c.d.
409*4=1636
904*4=3616
@apartado (12 stycznia o godz. 10:42 193838)
To max przy N=11, a min?
@apartado (13 stycznia o godz. 21:01 193839)
Ale taki schemat szybko się załamie przy rosnącym N, tzn. wydaje się że można dość łatwo generować l. biograficzne przy N=11,12,13,14,15,.. ale kolejne nie są prostymi kopiami poprzednich (z jednym zerem więcej i przesunięta jedynką) a trochę się różnicują. Analogicznie można schodzić z N*=max w dół i nawet jeśli widać schemat to można go kontynuować tylko przez parę kroków przypadków jest kilkadziesiąt.
Zauważmy, że przy N≤10 są 2 liczby autobio. dla N=4 ale żadnej dla N=6.
@Markoniusz
Tak na szybko, to nie widzę łatwej kontynuacji schematu dla N>13.
Poprosiłbym o jakiś przykład dla N=14 (?).
@Markoniusz
14 stycznia o godz. 21:47 193840
„lubimy jednoznaczność”.
Może nie jednoznaczność, ale czteroznaczność może zapewnić gramatyka:
2, 3, 4 dają „lata”, pozostałe zaś „lat”. Wtedy zostają cztery rozwiązania:
409*8=3272
904*8=7232
851*4=3404
356*4=1424
Można też dorzucić „największy” i „najmniejszy” rok, co już będzie jednoznaczne.
apartado
15 stycznia o godz. 13:20 193843
Proszę bardzo:
N=11: 72100001000
N=12: 821000001000
N=13: 9210000001000
N=14: 93010000010001
N=15: 940010000100011
….. ????
N=85: 9999999787888888877777666666666555555555444444444333333333222222222111111111000000000
N=86: 99999997888888889777777666666666555555555444444444333333333222222222111111111000000000
N=87: 999999988898888877777777666666666555555555444444444333333333222222222111111111000000000
N=88: 9999999988888888777777777666666666555555555444444444333333333222222222111111111000000000
N*=89: 99999999898888888777777777666666666555555555444444444333333333222222222111111111000000000
xswedc
17 stycznia o godz. 22:29 193844
Ha, sprytnie!
Niestety ramka zakrywa końcówki długich liczb autobio. 🙁
N=85: 9999999787888888877777666666666555555555444444444-
333333333222222222111111111000000000
N=86: 99999997888888889777777666666666555555555444444444-
333333333222222222111111111000000000
N=87: 999999988898888877777777666666666555555555444444444-
333333333222222222111111111000000000
N=88: 9999999988888888777777777666666666555555555444444444-
333333333222222222111111111000000000
N*=89: 99999999898888888777777777666666666555555555444444444-
333333333222222222111111111000000000