8 out
W dziewięciu jasnozielonych małych choinkowych trójkątach zawisło dziewięć różnych cyfr – wszystkie oprócz ósemki.
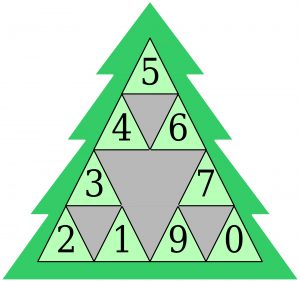
Sumy liczb w każdym kwartecie tych trójkątów przy brzegach choinki są różne (12, 14 i 18). A powinny być jednakowe. W tym celu należy przewiesić jak najmniej cyfr. Ile co najmniej i które? Niewykluczone, drogie dziatki, że można to zrobić na więcej niż jeden sposób.

Komentarze
Ręcznie znalazłem:
Trzy cyfry z trójkąta 406 można przestawić antyzegarowo.
Komputer podpowiedział jeszcze:
Trzy cyfry z trójkąta 462 można przestawić zegarowo.
Na razie znalazłem tylko jedno rozwiązanie, ale po sugestii, że może być ich więcej, jestem niemal pewny, że nie jest poprawne. 🙁
Moje sumy to 15. Zamienione są cztery cyfry: 1, 2, 5 i 7:
http://pokazywarka.pl/bez8/
Znalazłem dwa rozwiązania, w których 6 bombek pozostaje na miejscu a 3 podlegają permutacji:
___5__________5
__6_0________2_4
_3___7______3___7
2_1_9_4____6_1_9_0
W pierwszym przypadku należy przewiesić cyklicznie bombki z liczbami 4, 6 i 0, a w drugim: 4, 6 i 2
Znalazłam 11 rozwiązań, z czego w dwóch można zostawić 6 cyfr na poprzednich miejscach. Zgodnie z ruchem wskazówek zegara:
5074 – 4912 – 2365
5470 – 0916 – 6325
Sumę 16 przy każdym boku trójkąta otrzymamy przy zamianie miejscami trzech cyfr 0,4,6 albo 2,4,6.
Miałem dobre przeczucie, że zadanie jest chytre. Między uszkami, a pyskiem karpia znalazłem dwa rozwiązania tylko z trzema zamienionymi cyframi: 2, 4, 6 i 0, 4, 6 oraz sumą 16.
http://pokazywarka.pl/bez8a/
Jestem też na 99,99% pewny, że najmniejsza możliwa suma, to 15. Ale, czy rzeczywiście nie da się zrobić czternastki?
Można, w odpowiedni sposób, przewiesić między sobą następujące trójki liczb:
(2, 4, 6) lub (0, 4, 6)
i wówczas sumy przy bokach choinki będą jednakowe, czyli równe 16.
…………………………………………………..
Skoro już jesteśmy przy sumach, to w grudniowym „Umyśle giętkim” (12/2019) pojawiła się wzmianka o grze liczbowej autorstwa Johna Conwaya.
Zasady gry wydały mi się jasne dopóki nie pojawił się przykład pewnej rozgrywki:
1) N (nieparzysty) zaczyna ruchem 3;
2) P (parzysty) odpowiada 4;
3) N podaje 5 i wygrywa, bo wszystkie pozostałe liczby (którymi mógłby odpowiedzieć rywal) zawarte są we wzorze: 3x + 4y + 5z.
Moje pytanie brzmi. Dlaczego P nie może odpowiedzieć 2 (dwójką)?
Oczywiście, że może – i wygra. Podany przykład ilustruje błędny ruch gracza P.
mp
Są dwa rozwiązania z zamianą trzech bombek:
5 2 4 3 7 6 1 9 0
5 6 0 3 7 2 1 9 4
Bombki zawieszamy od góry i od lewej.
Jest jeszcze jedno, w którym zdejmujemy 0 w to miejsce przewieszamy 2 a na miejsce 2 zawieszamy 8 (jeżeli 8 jest w komplecie). Czyli zmieniamy miejsce powieszenia tylko jednej bombki.
6, 4 i 0 wsiadają na karuzelę lewoskrętną. Sumy 16.
@xswedc
Moim zdaniem sumy 14 nie ma. Jest jedna 15, cztery 16, dwie 17, jedna 18 i trzy 19.
Sumy 14 nie ma na pewno. Zakładam, zgodnie z zadaniem, że liczby nie mogą się powtarzać. Suma liczb od 0 do 9 z pominięciem 8 to 37. Najbliższa, większą liczbą podzielna przez 3 to 39, do uzyskania której wymagane byłoby użyć powtarzających się liczb. Kolejna to 42, która podzielona na 3 da 14.
42-37=5, co można uzyskać poprzez umieszczenie w rogach liczb 0 1 4 lub 0 2 3.
Przeanalizujmy rząd liczb zawierający 9.
14-9=5
Sumę 5 można uzyskać poprzez użycie liczb 0 1 4 lub 0 2 3. Są to więc te same liczby, które muszą być umieszczone w rogach. Nie możemy umieścić ich zarazem w jednym rzędzie i w trzech rogach. Cbdu