Ostatni cesarz Shikaku
Dałbym już spokój shikaku i zajął się jego znacznie młodszym, a mało znanym krewniakiem, gdyby nie komentarze kilku osób, dotyczące zadania z poprzedniego wpisu, w rodzaju Piotrowego S.: „zadanie jeszcze łatwiejsze od poprzedniego”. Ponieważ poza tym na trudność żadnego shikaku, także tego ze strony Thomasa Snydera, nikt nie narzekał – wręcz przeciwnie, pojawiło się nawet określenie „banalne” – więc upewniło mnie to w przekonaniu, że shikaku należy do typów łamigłówek, że tak powiem, prostych z natury albo immanentnie i permanentnie. Nie dość, że zawsze na początku w diagramie musi się trafić jakiś prostokąt-pewniak, to w trakcie rozwiązywania bez kłopotu, krok po kroku, można oznaczać kratki-pewniaki, które muszą zostać objęte jakimś konkretnym prostokątem, a prostokąty nietrudno zamykać. Droga do celu jest więc gładkim lub tylko odrobinę wyboistym spacerkiem, bo układając zadanie, dużych wertepów, zagrażających połamaniem głowy, sprokurować nie sposób. Wędrówka może być co najwyżej długa i żmudna, jeśli diagram ma rozmiary XXL.
Wyszperałem w archiwum shikaku, które wygląda na najtrudniejsze z tych, jakimi dysponuję. Małe nie jest, ale i tak mniejsze niż Snyderowe.
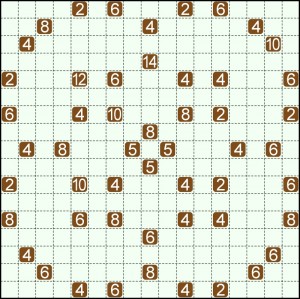
Proponuję zacząć od testu spostrzegawczości, czyli wypatrzyć w diagramie wszystkie prostokąty-pewniaki (ile ich jest?). A kogo wymiary nie przestraszą, czyli przystąpi do dzielenia i dotrze do mety, tego odpowiedź na pytanie: w ilu miejscach krzyżują się linie dzielące? – będzie mile widziana. Równie wdzięczny będę za ocenę, czy zadanie jest bardziej trudne, czy bardziej żmudne.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.

Komentarze
Pewniaki dostrzegłem dwa: w lewym górnym rogu ósemka i w lewym dolnym szóstka.
Dwa miejsca: 2, 6, 6, 12 oraz 4, 6, 10, 14
Zadanie nie sprawia większych trudności. Po wstawieniu kilku prostokątów jakoś to leci i tylko czasami trzeba na chwilkę się zatrzymać, aby dostrzec coś, co jest raczej oczywiste.
Pozdrawiam
Po pierwszym rzucie oka widzę dwa rogi pewniaki: lewa góra i dół, A jeśli chodzi o dół to z lewa na prawo można rozwiązywać bez żadnego wysiłku.
Linie podziału krzyżują się w dwóch punktach. Pewniaki to – prostokąt o polu 8 w lewym górnym rogu i o polu 6 w lewym dolnym rogu.
Trudne zadanie nie jest. Różni się od poprzednich w tym, że nie dałem rady dzielić pól na całe prostokąty od razu, musiałem się wspomóc prostokątami pewnymi, ale niepełnymi. Bardziej więc żmudne…
Jeśli umiem liczyć, to znalazłem 2 skrzyżowania, a pewniaki są min. 2 – 8 w lewym górnym rogu i 6 w lewym dolnym.
Pewniaki sa trzy: lewy gorny rog (8), lewy dolny rog (6), prwy gorny rog (10). Rozwiazywanie idzie prawie jak po masle. Nie jest ani trudne, ani zmudne. Skrzyzowania sa dwa.
a
To zadanie również jest dość łatwe i jedynie odrobinę bardziej żmudne od poprzedniego. W diagramie występują 2 skrzyżowania. Jeśli chodzi o pewniaki to jest nim 8 w górnym lewym rogu. Dalej 6 w dolnym lewym rogu. Po 6 oczywista staje się 4 obok.
Tym razem zacząłem od środka. Znalazłem pewniaka logicznego – prostokąt o polu 10. Nie szukałem następnych, bo później poszło jak z płatka. Są dwa miejsca, w których krzyżują się linie dzielące.
http://pokazywarka.pl/7yolu9/
Łatwe. Znalazłem 2 pewniaki: 8 po lewej u góry i 6 po lewej na dole.
Dwa punkty przecięcia.
Zadanie nie jest trudne, ani żmudne, ale przyjemnie się je rozwiązuje.