Podstępnie

Łamigłówki bywają podstępne. Podstęp niejedno ma imię, a jego ofiarą może paść nie tylko rozwiązywacz, ale także układacz. Piszę to jako autor i ofiara pewnego zadania z aktualnego Omnibusa wakacyjnego, które mnie przechytrzyło w niecny sposób. Chciałem, aby było najprostszym z serii trzech tego samego rodzaju, a ono wykorzystało moje dobre intencje i złośliwie poczęstowało mnie pewną dodatkową „atrakcją”.
Przechodząc do konkretów:
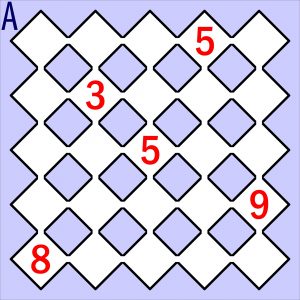
W białych polach diagramu znajduje się pięć czerwonych cyfr. W pięć innych należy wpisać pięć czarnych cyfr – różnych, od 1 do 5 (w przykładzie czerwonych i czarnych są po cztery). Ich rozmieszczenie powinno spełniać następujące warunki:
– w każdym wierszu i w każdej kolumnie powinna znaleźć się dokładnie jedna czarna;
– każda czerwona musi być równa jednej czarnej lub sumie dwóch czarnych widocznej (widocznych) z pola czerwonej, patrząc w rzędzie lub/i kolumnie (inna czerwona zasłania widok – jak w przykładzie czerwona czwórka zasłania czerwonej dwójce wpisaną czarną trójkę).
Przykład


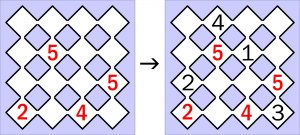
Figlem, który spłatała łamigłówka (oczywiście z moją pomocą) okazała się większa niż jedno liczba rozwiązań.
I stąd się bierze moje pytanie:
ile rozwiązań ma to zadanie?

Komentarze

[xswedc]

Dwa możliwe położenia piątki, a dla każdego z nich po dwa dla czwórki, co daje cztery rozwiązania:
http://pokazywarka.pl/podstepnie/

[logi]

4 rozwiązania

[OlaGM]

Znalazłam 4 rozwiązania.

[tomash]

Dzień dobry,

są cztery rozwiązania, wychodząc od 5 i 3 idzie jak po sznurku.

(poniżej tylko czarne)
-2—
–1–
—-4
5—-
—3-

—-4
—1-
-2—
5—-
–3–

3—–
—2-
-1—
–4–
—-5

-1—
–2–
3—-
—4-
—-5

Pozdrawiam,

[Michał S]

Są 4 rozwiązania.
Skoro suma czerwonych liczb to 30, każda czarna musi być widziana 2 razy. Czarna 5 musi być w wierszu 9 i kolumnie 8 lub na odwrót. Stąd wniosek, że 5 jest albo w pierwszej kolumnie przedostatniego wiersza (a wtedy 4 musi być w ostatniej kolumnie w pierwszym lub trzecim wierszu) albo w ostatniej kolumnie ostatniego wiersza (a wtedy 4 musi być w przedostatnim wierszu, w trzeciej lub czwartej kolumnie). Dla każdego z tych czterech przypadków czarną 3 trzeba umieścić na przecięciu linii, przechodzących przez 8 i drugą 5 (czyli tę, która nie jest w linii z 4). Zostaje już tylko odpowiednio umieścić 2 i 1, co zawsze uda się zrobić.

[Spytko z Melsztyna]

Są cztery rozwiązania.
Zadanie robi się łatwe po zauważeniu, że suma czarnych cyfr jest dokładnie dwa razy mniejsza od sumy czerwonych cyfr.
Konsekwencją tego jest uproszczenie drugiego warunku (każda czerwona musi być sumą dwóch czarnych).
Następnie zauważamy, że 5 może wystąpić tylko na dwóch polach. Startujemy więc od piątki i idziemy jak po sznurku znajdując drugą składową sumy w każdym kroku.
Pojawiają się tylko dwa rozwidlenia w drugim kroku dla każdego przypadku piątki co daje 2 razy 2 = 4 rozwiązania widoczne pod poniższym linkiem:
http://pokazywarka.pl/y4g5e7/

[Wiąz]

Znalazłem 4 rozwiązania:
===54
=3=1=
=25==
5===9
8=3==

=2=5=
=31==
==5=4
5===9
8==3=

=1=5=
=32==
3=5==
===49
8===5

3==5=
=3=2=
=15==
==4=9
8===5

[apartado]

Wygląda na to, że 4 sztuki.

0 0 0 0 4
0 0 0 1 0
0 2 0 0 0
5 0 0 0 0
0 0 3 0 0

0 2 0 0 0
0 0 1 0 0
0 0 0 0 4
5 0 0 0 0
0 0 0 3 0

3 0 0 0 0
0 0 0 2 0
0 1 0 0 0
0 0 4 0 0
0 0 0 0 5

0 1 0 0 0
0 0 2 0 0
3 0 0 0 0
0 0 0 4 0
0 0 0 0 5

Komputerowo, żeby potrenować debugging, który to bug się zdarzył (jestem rozmarzony) i ukrywał jak tylko potrafił – był perfidny i podstępny, bo ukrył się leżąc na wierzchu – tak czy owak warto było 😉

[Antyp1958]

Znalazłem 3 rozwiązania:
x1xxx
xx2xx
3xxxx
xxx4x
xxxx5

3xxxx
xxx2x
x1xxx
xx4xx
xxxx5

x2xxx
xx1xx
xxxx4
5xxxx
xxx3x

[Antyp1958]

Jest i czwarte rozwiązanie
xxxx4
xxx1x
x2xxx
5xxxx
xx3xx