Raz 2
Jak wynika z Państwa komentarzy, wsparcie komputerowe okazało się zbędne przy rozwiązywaniu zadania liczbowego zamieszczonego w poprzednim wpisie. Wśród znajomych wytrawnych rozwiązywaczy znalazła się nawet osoba, która poinformowała mnie, że rozwiązała to zadanie w głowie przed zaśnięciem. Wierzę, że tak było – tym chętniej, że delikatne (!) główkołamanie na dobranoc uważam za znakomity środek nasenny i antidotum przeciw myśleniu w takich sytuacjach o kłopotach i głupotach. Kontynuując ten wątek logiczno-rachunkowy proponuję coś w podobnym stylu.
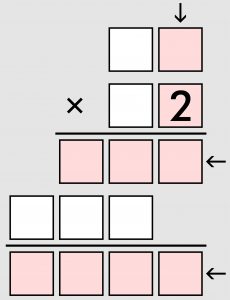
Cyfry w słupkowym zapisie mnożenia zastąpiono kratkami; ujawniona jest tylko jedna. Należy rozszyfrować działanie, korzystając z podpowiedzi: w każdym rzędzie kratek wskazanym strzałką (czterech kratek w pionie, trzech i czterech w poziomie) suma cyfr jest taka sama.
Tym razem chyba na pewno 🙂 nie trzeba będzie korzystać z komputera, choć zapewne przyda się kalkulator.

Komentarze
96 x 32=3072
Rozwiązanie jest jedno:
__96
_x32
——
_192
288
——
3072
Przy pomocy programu sprawdziłem czy na miejscu 2 może być inna liczba (pozostałe warunki bez zmian). Wyszło, że 2 można zamienić na 3 i dalej jest jedno rozwiązanie:
97×93=(291 873)= 9021.
Metodą prób i błędów po kilku minutach natrafiłam na 96 x 32 = 3072.
Ja nawet się zawziąłem, żeby to w pamięci zrobić: najpierw stwierdzamy, że pierwsza 3-cyfrowa liczba pod kreską musi mieć na początku 1, co eliminuje wiele możliwości jeśli chodzi o prawą kolumnę, bo np. 4×2 daje 8 i potem jeszcze raz 8, a więc w sumie 22, czyli suma cyfr liczby pod kreską musiałaby być 1+x+8 = 22, odpada. Dwie możliwości jakie zostają to 6 i 1, wtedy pierwsza liczba zadana jest jednoznacznie jako odpowiednio 96 i 71, a sumy o które chodzi są odpowiednio 12 i 7 (96*2 = 192, 71*2 = 142). Akurat zacząłem sprawdzać od 71, no więc to w ogóle nie wychodzi. A w przypadku 96 udaje się niemal od razu: 96*32 = 3072, suma wszędzie 12. Ciekawy punkt, czy w ogóle sprawdzać 22: wtedy druga liczba pod kreską miałaby sumę taką samą i układający zadanie nie omieszkałby wskazać, że cztery sumy są identyczne, a nie trzy 🙂 No ale nie musiał, mógł wskazać trzy dla zmylenia przeciwnika, tak więc sprawdziłem, ale nie pasuje. Potem jeszcze pozostało sprawdzić, czy to jedyne rozwiązanie, 42 nie pasuje, a od 52 suma dwóch pierwszych cyfr wyniku robi się już bardzo duża, więc 32 jest jedyne.
96 * 32 = 3072
Ołówek i kalkulator wystarczy.
96
32
——
192
288
——
3072
Mam nadzieję, że się tekst nie rozjedzie.
Nie udało mi się bez komputera (ale nie programowałem tylko używałem Excel’a). Zauważyłem tylko, że taka sama suma musi być 7,12,17,22 (2 i 27 odpadają)
Rozwiązanie to:
96 * 32 = 3072
Pozdrawiam,
Weekend, pora na przyjemności 😉 Ale mam zagwozdkę z tym zadaniem.
Można dość łatwo wydedukować dopuszczalne wartości mnożnej spełniające część warunku zadania: 10; 35; 42; 71; 96.
Łatwo też widzieć, że w każdym z tych przypadków mnożnik 2 jest rozwiązaniem „zdegenerowanym” (1-cyfrowym), a w przypadku mnożnej 10 jest to jedyne rozwiązanie.
W celu znalezienia rozwiązań „regularnych” mnożników 2-cyfrowych najprostsza jest droga rachunkowa tj. dla każdej z 4 wartości dopuszczalnych mnożnej sprawdzenie wartości pierwszej cyfry mnożnika, w sumie 4*9=36 przypadków. Otrzymamy 4 rozwiązania regularne zadania: 35×92; 42×32; 42×62; 96×32.
Czy jednak to jest rozwiązanie dopuszczalne? Można to zrobić za pomocą kalkulatora ale jest to jednak rozwiązanie „siłowe”. Alternatywna analiza logiczna wydaje się b. mozolna wobec skomplikowanej zależności cyfr iloczynu od cyfr czynników i mnogości przypadków do rozpatrzenia.
Ciekawe czy jest tu jakiś sprytny skrót?
Ja mam małą zagadkę: dzisiaj Walentynki wypadają w Środę Popielcową. Kiedy poprzednio mieliśmy taką zbieżność i kiedy będzie tak następnym razem?
Między następnym a poprzednim rokiem z Walentynkową ŚP jest dystans 79 lat.
mp
To ja też mam zagadkę 😉 Gdy byłam w liceum, walentynki wypadły w tłusty czwartek. Ile lat minęło od tamtej pory?
I wszyscy rzucili się do rozwiązywania, żeby ustalić, ile lat (mniej więcej) ma Pani Ola. Ja już wiem, ale chyba nie wypada podawać rozwiązania :).
mp
@ aps1968 + w nawiązaniu do słów Gospodarza:
Czas do następnego jest około 12 razy krótszy niż do poprzedniego.
Mam tyle lat, że już mi chyba pamięć szwankuje 🙂
Chyba że na wikisource są błędy. Zajrzałam do tych tablic:
https://pl.wikisource.org/wiki/Tablice_%C5%9Bwi%C4%85t_ruchomych
i tam nie ma tłustego czwartku 14 lutego w latach mojego chodzenia do liceum.
@OlaGM
Takie wydarzenie miało też miejsce między 4 a 7 klasą tzw. podstawówki.
Wygląda na to, że Panowie dobrze rozwiązali – w poprzednie popielcowe Walentynki w Europie i nie tylko było dość dramatycznie, jak będzie w następne, nie wiadomo, ale niedługo się przekonamy, miejmy nadzieję wszyscy.
Zaciekawił mnie fakt, że mamy w tym roku zbieżność: jeśli ŚP w Walentynki, to Wielkanoc w Prima Aprilis. Musi tak być, jeśli oczywiście rok nie jest przestępny. Okazuje się, że jednak wcale często jest.
@OlaGM – jesli to był ostatni taki tłusty czwartek, to wygląda na to, że też wtedy byłem w liceum 🙂
Za to za naszego życia, zakładając że wszyscy mamy mniej niż 105 lat, raz tylko tłusty czwartek wypadł w styczniu, można sprawdzić, to bardziej ciekawostka niż zagadka.
@aps1968 – jesli to był ostatni taki tłusty czwartek, to wygląda na to, że też wtedy byłem w liceum
W ostatni walentynkowy tłusty czwartek (WTC) miałam jeszcze jednocyfrową liczbę lat 🙂 Za moich czasów licealnych WTC nie było, coś mi się musiało pomylić…
@OlaGM
Wpisywałem nie widząc jeszcze komentarza o pomyłce 🙂
Czyli jeśli ktoś „rzucił się do rozwiązywania, żeby ustalić”, musi troszkę zweryfikować. W mojej sytuacji niestety było to jednak liceum. Z tym że chyba wtedy jeszcze w ogóle nie obchodziło się Walentynek (przynajmniej w tym moim liceum :))