Gwiazdkowo
Gwiazdki w łamigłówkach mają niemal zawsze znaczenie formalne, tzn. są tylko znakami, które równie dobrze mogłyby być kółeczkami, krzyżykami itp. Gwiaździstość istotna merytorycznie pojawia się chyba tylko w tzw. gwiazdach magicznych, czyli gdy na liniach tworzących ramiona rozmieszczane są liczby. Spróbowałem sprostać wyzwaniu polegającemu na „umerytorycznieniu„ gwiazd i równoczesnym powiązaniu ich z nadchodzącym nowym rokiem. I wyszło coś takiego:
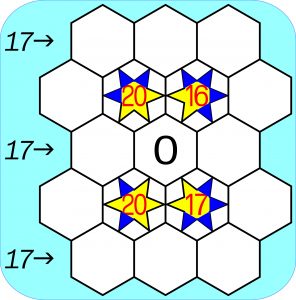
W pustych polach powinny pojawić się liczby od 1 do 12 (środkowe pole okupuje zero). Liczba w każdej z czterech gwiazdek jest sumą liczb, które powinny znaleźć się w polach, na które wskazują niebieskie ramiona gwiazdki. Ponadto 17 powinna być równa suma trzech liczb w każdym ze wskazanych rzędów.
Na moje oko zadanie jest nieproste, ale do ruszenia bez komputerowego wsparcia. Nie upierałbym się jednak, że rozwiązanie jest tylko jedno.
Zdrowia i spokoju dla wszystkich na Święta i rok nowy.

Komentarze
Ręcznie znalazłem dwa rozwiązania.
Rzędami:
10 1 6
9 4
12 0 5
11 3
8 2 7
i drugie:
10 1 6
9 4
12 0 5
11 3
8 7 2
Rozwiązania są dwa (kolejno wierszami):
10, 1, 6
9, 4
12, 0, 5
11, 3
I dwa warianty ostatniego wiersza:
8, 2, 7
8, 7, 2
Ostatnie dwie kratki wchodzą w skład tych samych sum (i żadne inne dwie kratki nie są w takiej sytuacji), więc na starcie można stwierdzić, że rozwiązań będzie parzysta liczba.
Wesołych Świąt!
A mnie się to zadanie wydaje bardzo łatwe. Akurat w sam raz dla kogoś, kto urządził Wigilię na 14 osób i koło północy poczuł, że musi odetchnąć przy jakiejś łamigłówce 😉
W środkowym rzędzie ma być suma 17 złożona z dwóch składników. Opcji jest tylko kilka 9-8, 10-7, 11-6 i 12-5. Szybko się okazuje, że tylko 12-5 pasuje. A wtedy reszta uzupełnia się jak po sznurku.
10 1 6
9 4
12 5
11 3
8 2 7 lub 8 7 2
Wesołych Świąt!
Rzędami:
10,1,6
9,4
12,0,5
11,3
8,2lub7,7lub2
10 – 1 – 6
9 – * – * – 4
12 – 0 – 5
11 – * – * – 3
8 – 7 – 2
7 i 2 mogą zamienić się miejscami.
Łatwe do zrobienia ręcznie przy niewielkim wsparciu komputera.
Puste pola oznaczamy od lewej do prawej i od góry w dół (tak jak byśmy czytali tekst), kolejnymi literami a,b,c,d,e,f,g,h,i,j,k,l.
Po chwili zastanowienia przyjmujemy jako zmienne niezależne a, d, f.
Reszta wygląda tak:
b=20-a-d
c=d-3
e=a+f-18
g=17-f
h nie jest związana żadną zależnością więc przypiszemy jej to co zostanie wolne
i=3
j=20-f
k + l = f-3
Teraz dla a, d i f, generujemy 1728 = 12^3 ciągów (z powtórzeniami dla prostoty algorytmu; można by jeszcze ograniczyć zakresy a,d, i f gdybyśmy chcieli robić tylko ręcznie).
Dla każdej takiej kombinacji a, d, f, obliczamy resztę zmiennych i sprawdzamy czy ich wartości mieszczą się między 1 i 12 oraz czy się nie powtarzają.
Wyskakuje niecałe 10 kombinacji i teraz sprawdzamy które sumy k+l daje się rozdzielić.
Jest tylko jedna taka możliwość co daje dwa rozwiązania bo k i l możemy zamienić miejscami.
Na samym końcu przydzielamy h pozostałą liczbę.
Są 2 rozwiązania:
a,b,c,d,e,f,g,h,i,j,k,l
10,1,6,9,4,12,5,11,3,8,2,7
10,1,6,9,4,12,5,11,3,8,7,2
Dowód na niejednoznacznosc rozwiązania:
Najniższy rząd, dwie komórki z prawej strony. Zamiana miejscami wartości tych dwóch komórek nie psuje żadnego z warunków na sume elementów.
Wesołych świąt…
Rozwiązania są dwa. Rzędami od góry
10 1 6
9 4
12 0 5
11 3
8 2 7
Drugie rozwiązanie otrzymamy po zamianie miejscami 2 i 7.
Pozdrowienia świąteczno-noworoczne.
Dla wszystkich, którzy zrobili Gwiazdki i łakną wyzwań proponuję zadanie pomostowe:
Znaleźć najmniejszą odległość między dwoma parabolami: f(x)=x^2+1/2 i g(x)=-(x-38)^2 oraz punkty dla których ona zachodzi.
Zabronione Monte Carlo i rachunek różniczkowy 2 zmiennych.
Pochodna jednej zmiennej i prosta geometria analityczna plus pomysł wystarczą, a może da się jeszcze prościej…..?
Znalezione ręcznie rozwiązanie:
-10–1–6-
-9–x–x–4
-12–0–5-
11–x–x–3
–8–2–7-
Drugie rozwiązanie (zgodnie z obserwacją z poprzedniego wpisu) powstaje poprzez zamianę miejscami wartości 2 i 7.
Komputer potwierdził, że innych rozwiązań nie ma.
Rozwiązanie (niestety komputerowe):
10 1 6
9 4
12 5
11 3
8 2 7
Wydaje mi się, że zadanie zyskałoby na „wnioskowalności” i radości rozwiązywania, gdyby rozróżnić pola z liczbami parzystymi i nieparzystymi.
Dodatkowo w tym przypadku zmniejszyłoby to ilość rozwiązań do jednego (patrz komentarz @miodzio).
Od razu widać, że na prawo od zera musi być 5, bo jest to najmniejsza
liczba, która daje sumę 17 w środkowym rzędzie, a zarazem największa,
przy której sumy czterech liczb w prawych gwiazdkach nie przekroczą 16 i
17.
Skoro 5 jest na prawo od zera, to 12 na lewo od zera i 8 w lewym dolnym rogu.
Prawa dolna gwiazdka ma liczbę 17, dwie liczby pod nią dają w sumie 9,
więc na prawo od tej gwiazdki musi być 3.
W dolnym wierszu muszą być liczby 2 i 7, w dowolnym porządku (jak
zauważył miodzio).
Przy prawej górnej gwiazdce muszą być liczby 1, 4 i 6. Ponieważ 7 i 12
są już wykorzystane, 17 w górnym wierszu daje tylko para 1 z 6, wraz z
liczbą 10. Zatem 4 jest na prawo od prawej górnej gwiazdki, a w górnym
wierszu mamy kolejno 10, 1 i 6, bo na lewo od lewej górnej gwiazdki musi
być 9.
Została tylko 11 i trafia ona do jedynego sześciokąta, nie wskazanego
przez żadną gwiazdkę.
Odcinek łączący najbliższe punkty będzie prostopadły do obu parabol.
f'(F) = 2F
Prosta prostopadła do f(x): ą(x) = -x/2F + a
Brakujący parametr wyznaczymy wiedząc, że krzywa i prosta przetną się w punkcie F: f(F) = ą(F)
-1/2 + a = F^2 + 1/2
a = F^2 + 1
ą(x) = -x/2F + F^2 + 1
To samo dla drugiej: g(x) = -x^2 + 76x – 1444
g'(x) = -2x + 76
ę(x) = x/(2*(G – 38)) + b
ę(G) = g(G)
G/(2*(G – 38)) + b = -G^2 + 76G – 1444
b = -(G-38)^2 – G/(2*(G – 38))
Ale, ale… ą(x) = ę(x), a więc ich parametry też są sobie równe:
Z współczynnika przy x:
-1/2F = 1/(2*(G – 38))
38 – F = G
Z wyrazu wolnego:
a = b
F^2 + 1 = -(G-38)^2 – G/(2*(G – 38))
F^2 + 1 = -F^2 – (38 – F)/(-2*F)
-2F^3 – 2F = 2F^3 – 38 + F
4F^3 + 3F – 38 = 0
F = 2
G = 36
f(F) = 4,5
g(G) = -4
Czyli szukane punkty, to: (2;4,5) i (36;-4), a odległość: ~35.
A teraz z innej beczki:
Na szachownicy o rozmiarach 4×4 rozmieszczono następujące wartości:
2112
3212
1323
3111
Na dowolnie wybranym polu stawiamy Hetmana szachowego, a następnie wykonujemy hetmańskie posunięcia o długości zgodnej z wartością aktualnie zajmowanego pola.
Należy odwiedzić wszystkie pola.
c.d.n
@Spytko z Melsztyna:
Fajne zadanie, ale nie chce mi się… 🙂
@y-b:
Myślałem podobnie, ale nie przelałem swoich myśli na papier…
@apartado:
To jest przypadek szczególny problemu znajdowania ścieżki Hamiltona w grafie… A to jest NP-trudne! 🙂
Rzędy to ABCD, a kolumny 1234. Hetman porusza się tak:
A2 – D2 – B4 – A4 – D1 – D3 – A3 – B2 – D4 – C4 – C3 – A1 – C1 – B1 – C2 – B3
@miodziu
chyba niezupełnie NP-trudny:
@OlaGM
Brawo ! – rozgrzewka zaliczona 😉
A może trochę większy rozmiar?
24412
33122
23113
33221
22124
proponuję oznaczenie pól jak tutaj:
https://en.wikipedia.org/wiki/Chessboard
Tak jak Miodziu – bezkarnie zamieniam 2 liczby w dolnym rzędzie.
Od góry:
10-1-6
9-4
12-(0)-5
11-3
8-2-7 lub 8-7-2
@y-b & miodziu:
Wzorcowe rozwiązanie 🙂 chyba trudno znaleźć lepszy sposób.
Dla uniknięcia konieczności myślenia można tą procedurę zapisać np. takimi wzorami:
1. f'(x1)=g'(x2)
2. f'(x1)*[(f(x1)-g(x2))/(x1-x2)]=-1
Dla parabol (czyli najprostszych krzywych nieliniowych) pojawia się równanie wielomianowe 3 stopnia.
Dla hiperboli i paraboli pojawi się równanie 7 stopnia, więc i tak trzeba przybliżać rozwiązanie.
@OlaGM:
A2-D2…..C2-B3 ?????? :/
Szachownicę oznaczamy:
abcd
efgh
ijkl
mnop.
Jest 75 hetmańskich dróg:
„gbfpoliehnmakcdj”
„bfpoliehnmakcgdj”
„ehpkacgbfnolimdj”
„ehnkacgbfpolimdj”
„ehnokacgbfplimdj”
„gliehpokacbfnmdj”
„liehpokacgbfnmdj”
„oliehpkacgbfnmdj”
„bfpokacgliehnmdj”
„gkacbfpoliehnmdj”
„kacgbfpoliehnmdj”
„akcgbfpoliehnmdj”
„bakcgfpoliehnmdj”
„okacgbfpliehnmdj”
„bakcgliehfponmdj”
„ehpolimdbfnkacgj”
„mdbfpoliehnkacgj”
„ehplimdbfnokacgj”
„mdbfpliehnokacgj”
„liehnmdbfpokacgj”
„bfnmdliehpokacgj”
„ehnolimdbfpkacgj”
„oliehnmdbfpkacgj”
„mdbfnoliehpkacgj”
„ehfnoplimdbakcgj”
„poliehfnmdbakcgj”
„opliehfnmdbakcgj”
„ehpolifnmdbakcgj”
„fpoliehnmdbakcgj”
„ehfpolinmdbakcgj”
„liehfponmdbakcgj”
„dbfpoliehnmakcgj”
„ehpokacgbfnmdlij”
„ehnmdbfpokacglij”
„ehfponmdbakcglij”
„ehnmakcgdbfpolij”
„ehnmdbakcgfpolij”
„ehpolimakcgdbfnj”
„ehpokacglimdbfnj”
„mdliehpokacgbfnj”
„ehpolimdbakcgfnj”
„mdbfpokacgliehnj”
„makcgdbfpoliehnj”
„mdbakcgfpoliehnj”
„mdbakcgliehfponj”
„ehplimakcgdbfnoj”
„ehpkacglimdbfnoj”
„mdliehpkacgbfnoj”
„ehplimdbakcgfnoj”
„mdbfpkacgliehnoj”
„makcgdbfpliehnoj”
„mdbakcgfpliehnoj”
„gdliehnmakcbfpoj”
„gliehnmakcdbfpoj”
„liehnmakcgdbfpoj”
„ehnkacglimdbfpoj”
„kacgliehnmdbfpoj”
„akcgliehnmdbfpoj”
„mdliehnkacgbfpoj”
„dliehnmakcgbfpoj”
„liehnmdbakcgfpoj”
„nmdbakcgliehfpoj”
„ehnmdbakcglifpoj”
„gbfnmakcdliehpoj”
„bfnmakcgdliehpoj”
„gkacbfnmdliehpoj”
„kacgbfnmdliehpoj”
„akcgbfnmdliehpoj”
„bakcgfnmdliehpoj”
„mdbfnkacgliehpoj”
„fnmdbakcgliehpoj”
„dbfnmakcgliehpoj”
„gbakcdliehfnmpoj”
„bakcgdliehfnmpoj”
„dbakcgliehfnmpoj”
i znajduje je program, który ma tylko 21 linijek 🙂
Od góry rzędami:
10,1,6
9,4
12,0,5
11 (liczba „bezrobotna”), 3
8, 7, 2 (lub 8, 2, 7)
Upierałbym się, choć głowy nie dam, że pomijając wymienność 2 i 7, jest to jedyne rozwiązanie. Bo 12 i 5 być musi, co implikuje 8 i 3, i dalej też jednoznacznie.
Teraz i ja mogę z czystym sumieniem złożyć wszystkim najlepsze życzenia z okazji Nowego Roku 2017 🙂 Jest to liczba pierwsza, zastanawiam się, który rok był ostatnio pierwszy, i który będzie następny.
@apartado
A czy rozwiązanie jest tylko jedno, czy też jest ich wiele?
Na początek ustaliłam, gdzie może być początek (2 pola) i gdzie koniec (też 2 pola). Przyznam, że możliwość istnienia wielu rozwiązań zniechęca do główkowania nad tym. Bo to oznacza, że nic/niewiele więcej się nie wydedukuje, ani że się nie wejdzie w ślepą uliczkę, bo może być różnie.
@apartado:
Odnośnie hetmańskiej ścieżki w kwadracie 5 na 5 komp znalazł jak dotąd 835 ścieżek kończących się literą L. Przykładowe jedno z nich to: pacysqbwzntvukmrfigjhdeol. Nasuwa się naturalne zadanie: Znaleźć kwadrat 4×4, 5×5 aby istniało tylko jedno rozwiązanie 🙂
@apartado:
Jest jeszcze 1637 ścieżek z końcem w O. Przykładowa „pdigjhbwznsqtvecyrfukamlo”.
@ Spytko z Melsztyna
> Nasuwa się naturalne zadanie: Znaleźć kwadrat 4×4, 5×5 aby
> istniało tylko jedno rozwiązanie
Zapewne potrzebny by był warunek dodatkowy dot. tego, jak trasa ma przebiegać, np. nigdy nie skręca pod kątem prostym albo nigdy nie zawraca (tzn. nie przebiega np. adb).
@OlaGM
Myślałem o odpowiednim dobraniu liczb w kwadracie. Muszą być odpowiednio duże aby graf nie miał zbyt wielu krawędzi. Jedynki powodują eksplozję rozwiązań. Być może w ten sposób nie da się uzyskać tylko jednej ścieżki i wtedy można wprowadzać jakieś ograniczenie na kształt drogi 🙂