Wieżowe podchody
Aby być wiernym logu Łamiblogu powinienem od czasu do czasu nawiązywać do szachów. Oczywiście nie ściśle szachowo, bo to nie główny temat blogu, tylko łamigłówkowo. Na szczęście logicznych zadań i problemów z szachowym entourage’em powstało mnóstwo. Jest wśród nich grupa zwana podchodami lub labiryntami. Jedną z takich łamigłówek prezentowałem przed laty tutaj. Pora na kolejną, różniącą się nieco regułami od poprzedniej.
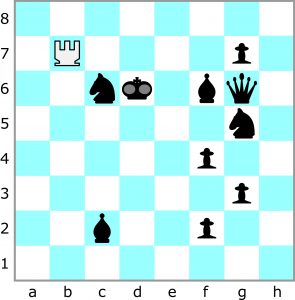
Słowo „podchody” ma kilka znaczeń. Tym razem chodzi o ukradkowe zbliżanie się do kogoś lub czegoś. W poniższym zadaniu ruchy wykonuje tylko biała wieża. Pozycja czarnych jest od początku do końca niezmienna, statyczna. Po żadnym ruchu wieża nie może znaleźć się pod biciem, ale jej ruchy mogą być biciami czarnych figur. Celem wieży jest takie podejście do czarnego króla, by mogła go bezpiecznie zaszachować – i aby zaszachowała. „Bezpiecznie” oznacza, że nie może być natychmiast zbita, a więc jedynym ratunkiem dla zaszachowanego króla byłaby ucieczka, czyli ruch na nieatakowane pole albo zasłona.
I jeszcze jeden istotny warunek: wieżowe podchody powinny składać się z minimalnej liczby ruchów.

Komentarze
Chodzi tylko o szacha, nie o szacha mata?
Tak, wystarczy szach.
mp
11 kroków: http://pokazywarka.pl/is7wk3/
Czerwone kropki to pola zagrożone. Niebieska linia to trasa wieży. Wieża zbija 3 pionki.
Kolejne ruchy wieży:
b6,a6,a2,d2+
Podejrzanie łatwo to poszło.
Słowo „podejrzanie” z poprzedniego komentarza okazało się kluczowe.
(Moje rozwiązanie ma nazwę „Niewidzialny Goniec”)
Myślimy dalej 😉
Ja się odważę: b6-a6-a8-h8-h4-xf4-g4-xg3-g2-xf2-d2+.
Who dares, wins.
mp
b6,a6,a8,h8,h4,xf4,g4,xg3,g2,xf2,d2+
Bez bić nie da się dotrzeć do króla. Sprawdzamy więc, kogo możemy zbić bezkarnie i okazuje się, że wielkiego wyboru nie ma: F4. To ścieżki do króla nie daje, ale odblokowuje G3. Itd. aż do: B6, A6, A8, H8, H4, F4, G4, G3, E3, E2, D2 (11 ruchów).
Są trzy (cztery) rozwiązania.
b6, a6, a8, c8, c4, bije f4, g4, bije g3, g2, bije f2, d2 szach
albo pierwsze trzy ruchy tak samo a następnie zamiast a8, c8 idziemy h8, h4 i dalej znów tak samo, albo po h8 (w drugim rozwiązaniu) idziemy h1, f1, bije f4 i dalej tak samo jak w pierwszym i drugim. Można jeszcze na siłę wskazać czwarte rozwiązanie …h1, c1, c4… 🙂
Jeżeli założymy, że czarne zaczynały na górnej części szachownicy (rząd 8 i 7) to 11 ruchów:
b6, a6, a8, h8, h4, f4, g4, g3, g3, f2, d2
11 ruchów:
b6, a6, a8, h8, h4, f4 (bicie piona), g4, g3 (bicie piona)
i dwie możliwe końcówki:
e3, e2, d2 lub g2, f2 (bicie piona), d2
http://pokazywarka.pl/u20h4i/
Mamy takie rozwiązanie: B6, A6, A8, H8, H4, F4x, G4, G3x, G2, F2x, D2.
Razem 11 ruchów.
Rozwiązał Adam, zapalony szachista (8 lat) z małą pomocą taty 🙂
@OlaGM – c3 jest zagrożone.
Ponieważ zadanie było chyba łatwe, więc dla wszystkich chętnych (i potrafiących się zaszyć przed przedświąteczną krzątaniną 🙂 ) podaję zadanko:
Jaś rzuca dwoma albo trzema kostkami z jednakową częstością.
Po którymś rzucie stwierdził: wypadło mi razem 10 oczek.
Jakie jest prawdopodobieństwo, że Jaś rzucał właśnie dwoma kostkami ?
b6-a6-a8-h8-h4-f4-g4-g3-g2-f2-d2
szybciej się chyba nie da
Spokojnych Świąt Panie Marku !
@Spytko z Melsztyna
3/30
czyli 0.1
inaczej mówiąc 10%
… ale możliwe (prawdopodobne), że moje rozwiązanie nosi nazwę „Niewidzialna Kostka”.
Nie wygląda mi to na najmniejszą możliwą liczbę ruchów, ale może tak:
b6, a6, a3, c3, c4, f4, c4, c3, g3, g2, f2, d2+
@Spytko:
jeśli Jaś rzucał z jednakową częstością dwoma lub trzema kostkami, a sumę 10 może mieć i na 2 i na 3, to prawdopodobieństwo, że rzucał dwoma jest 50%. Chyba, że nie dostrzegam jakiegoś haczyka.
P(2) = 3/36 = 18/216
P(3) = 27/216
Bayesem go!
Albo proporcjami, skoro jednakowo często. Wyszło: 40%
To ja rzucę wyzwanie: Jaś rzuca naprzemiennie dwoma i trzema kostkami (pierwszy rzut dwoma). Znowu stwierdza, że ma 10 oczek i jakie teraz mamy prawdopodobieństwo? 😉
Można pójść i dalej: Jaś rzuca naprzemiennie dwoma i trzema, wreszcie pierwsza dycha wypadła na dwóch kostkach. Jakie jest prawdopodobieństwo, że pierwszy rzut był dwoma kostkami? (tego już mi się nie chciało liczyć 😉 )
Jaś rzuca nieskończoną liczbą kostek: K_1, K_2, …
Dla pewnych n i m suma K_n + K_(n+1) + … + K_m = 10 i jest to najmniejsze m spełniające ten warunek.
Jakie jest prawdopodobieństwo, że m – n = 1?
Tutaj wystarczy mi odpowiedź, czy to zadanie dla człowieka 😉
@jukka2003
Dzięki za wskazanie błędu. Gratuluję Adasiowi 😉
Zatem proponuję takie rozwiązanie, również w 11 krokach:
http://pokazywarka.pl/6migxd/
@Spytko z Melsztyna
P-wo wyrzucenia sumy 10 rzucając dwiema kostkami to 3/36 = 1/12
P-wo wyrzucenia sumy 10 rzucając trzema kostkami to 27/216 = 1/8
A – zdarzenie polegające na tym, że Jaś rzucał dwiema kostkami.
A’ – zdarzenie przeciwne do A, tzn. Jaś rzucał trzema kostkami.
B – zdarzenie polegające na tym, że Jaś wyrzucił dokładnie 10 oczek.
Oczywiście P(A) = 1/2 oraz P(A’) = 1/2
P(B) = P(A) * 1/12 + P(A’) * 1/8 = 1/2 * (1/12 + 1/8) = 1/2 * 5/24 = 5/48
P-wo zajścia zdarzenia A, pod warunkiem wystąpienia zdarzenia B dane jest wzorem:
P(A|B) = P(A i B) / P(B)
przy czym P(A i B) = 1/2 * 1/12 = 1/24
czyli
P(A|B) = (1/24) / (5/48) = 48 / 120 = 2/5
Mój komentarz zniknął… To jeszcze raz: dziękuję Jukka za wskazanie błędu i gratuluję Adasiowi. Moja nowa propozycja też ma 11 kroków:
http://pokazywarka.pl/p8whzd/
Pani Olu, nie zniknął, czeka na akceptację przed następnym wpisem, bo jest w nim rozwiązanie.
mp
To ja też dorzucę coś od siebie: „Idą kaczki, jedna za drugą. Ile ich jest?”
Zadanie o kostkach:
Z tego wszystkiego w wolnej chwili napiszę jakieś małe MonteCaro.
Bo intuicja mi mówi, że 40%-50% to za dużo.
Dużo za dużo.
Czy nie chodziło przypadkiem o Monte Carlo?
mp
b6, a6, a4, f4, g4, g3, g2, f2, d2
(na marginesie – zastanawia mnie pion na g7)
Wb6, a6, a8, h8, h4, :f4, g4, :g3, g2, :f2, d2+
Mam dwa warianty o jeden ruch krótsze:
b6, a6, a3, c3, c4, f4, g4, g3, g2, f2, d2+
albo dookoła
b6, a6, a8, h8, h4, f4, g4, g3, g2, f2, d2+
@ miodziu: trzy 🙂
To w podobnym stylu, ale mniej matematycznie:
A wróbelek na gałęzi siedzi czy stoi?
10.
B6;A6;A8;H8;H4;G4;G3;G2;F2;D2
kostki:
Dziękuję za poprawkę: oczywiście chodziło o Monte Carlo- to ten pośpiech który spowodował, że nie pochyliłem się nad tymi kostkami dłużej niż 2 minuty- stąd zła odpowiedź.
Monte Carlo mówi 40% i tego się będę trzymał 😉
@ miodziu:
Z tekstu jasno wynika, że kaczki są tylko dwie 🙂
@bubekró
pole a4 jest chronione przez Gońca z c2
(pion z g7 ogrywa istotną rolę w zmniejszaniu zasięgu kontroli swojej grupy)
@kroQ
pole g3 jest chronione przez piona z f4
Rozwiązania schematem Bayesa są oczywiście usprawiedliwione 😉 Ale chodziło mi o sprowokowanie bezpośredniego ataku na problem.
Skoro P(10 w 2 kości)=3/36 a P(10 w 3 kości)=27/216 to zapisujemy P(10 w 2 kości)=3/36=(6/6)*(3/36)=18/216. No i mamy P(Jaś rzucał 2 kościami)=18/(18+27)=2/5.
@Spytko z Melsztyna
Zauważam korzystanie z niewidzialności Skoczka c6,Gońca c2 oraz piona f2.
W moim pierwszym rozwiązaniu tez użyłem tej możliwości 😉
@czwartex
Pole c3 jest chronione przez Gońca f6
@miodziu
Ładny zielony wariant końcówki.
@miodziu: na zielony wariant skoczek nie pozwoli
@spytko: skoro za drugą kaczką jest jedna to razem są trzy (no bo jeszcze przed drugą jest jeszcze ta pierwsza)
@Spytko z Melsztyna
Zielony wariant @miodzio jest OK – kontrolowane przez Skoczka pole f3 nie jest wykorzystywane.
Przy okazji:
Gdyby w układzie początkowym dodać czarnego piona na e3 to zadanie miałoby jedno rozwiązanie.
@apartado
Rzeczywiście, rozjechałem tego skoczka nielegalnie, chociaż stoi tam jak wół 🙂
Umknął mi też elegancki, zielony (pacyfistyczny 😉 ), wariant Miodzia.
@stud
Skoro mówisz:”…jeszcze przed drugą jest jeszcze ta pierwsza”, to znaczy,
że kaczki gonią w piętkę: jedna za drugą i druga za pierwszą.
Są więc dwie kaczki, które gonią się po okręgu 😉
Oto do jakich, talmudycznych, sporów może prowadzić dosłowna interpretacja idiomów 🙂
@czwartex:
Wróbelek… hehe… na pewno nie leży 🙂
@Spytko z Melsztyna:
Tylko dwie kaczki?
@apartado:
Dziękuję
@stud:
A czemu niby skoczek miałby nie pozwolić na zielony wariant? Może czegoś nie widzę?
@czwartex
No właśnie nie, bo gdybyś miał informację, że wypadło mu w sumie np. 13, to wiedziałbyś na pewno, że na 100% rzucił trzema. W tym sensie informacja o sumie jest ważna.
@wszyscy
Przypomina mi to klasyczne zadanie, że porwał cię potwór i postawił przed trojgiem drzwi. Za jednymi jest wolność, za dwojgiem kat czeka z toporem. Potwór wie, które drzwi są które, ty nie. Twoim zadaniem jest wskazać jedne drzwi, potwór następnie wskazuje inne niż wskazane przez ciebie, takie za którymi na pewno jest kat. I teraz twoja decyzja: albo pozostajesz przy wyborze pierwotnym, albo decydujesz się na trzecie drzwi, których nie wskazał potwór. Przy którym wyborze masz większe szanse się uratować, a może są one 50 na 50?
@aps1968:
Odnośnie potwora to wszystko rozstrzyga się przy pierwszym wyborze. 1/3 wybieramy wolność i 2/3 kat. w pierwszym przypadku wygrywa strategia „nie zmieniamy” w drugim wygrywa „zmieniamy”. czyli stosując strategie „zmieniamy” będziemy wygrywać w 2/3 przypadków.
Idą kaczki siedem za drugą, ile ich jest ? Odp: 9. Tu nie ma żadnych wątpliwości. Teraz zamieniamy 7 na „jedna” i wychodzi 3 kaczki 🙂 To chyba najprostsze wyjaśnienie tego zadania.
@Spytko
No właśnie, bo jeśli mamy pozostać przy pierwotnym wyborze, to ruch potwora w ogóle nie ma znaczenia, czyli zostaje 1/3. Za to jeśli chcemy ruch potwora uwzględnić, to mamy stuprocentową pewność – pod warunkiem, że pierwsze nasze wskazanie jest na kata. Na co szansa wynosi 2/3.
Albo kaczki jedna za siódmą, to wiadomo, że 8 🙂
@aps1968
Mówiąc jeszcze inaczej: Jeśli wybraliśmy kata to trzeba zmienić, jeśli wybraliśmy wolność to nie zmieniamy. Ponieważ kata wybieramy z p-wem 2/3 więc trzeba stosować strategię dobrej zmiany 🙂