Samotnik mini
Podstawowa zasada jest prosta: jeśli dwa pionki stoją obok siebie, to jednym z nich można przeskoczyć przez drugi i usunąć przeskoczony.
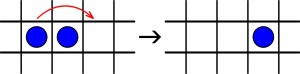
Wypadałoby dodać, że cała „akcja” ma miejsce zawsze w rzędzie lub kolumnie (nie na ukos, jak w warcabach) i zawsze w obrębie trzech kolejnych kratek. Taki skok-bicie jest typowe dla samotnika, wielochodowej łamigłówki trącącej myszką, rozwiązywanej (rozgrywanej) na planszy w kształcie krzyża. Jej prostsze, mniej żmudne warianty pojawiają się do dziś. We wszystkich występuje podstawowa zasada bicia przez przeskoczenie; wspólny jest także cel: wykonując serię bić należy doprowadzić do sytuacji, w której na planszy pozostanie jeden pionek. Różne są tylko układy początkowe i rozmiary planszy. Najmniejsza kwadratowa, na której zabawa nie jest trywialna, to plansza 4×4, choć wiele umieszczonych na niej układów rozwiązuje się niemal automatycznie. Na przykład taki:
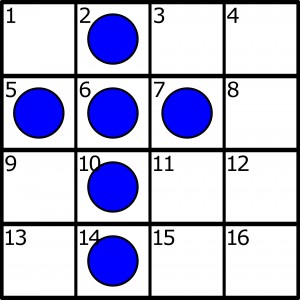
Rozwiązanie w pięciu ruchach:
1. 6-8
2. 14-6
3. 5-7
4. 8-6
5. 10-2 2-10
Czy z poniższym układem równie łatwo sobie Państwo poradzą?
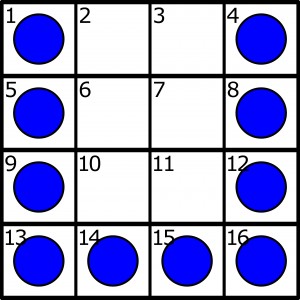
W tym przypadku konieczne jest wykonanie odpowiedniego wstępnego posunięcia – przeniesienia jednego pionka na puste pole, aby możliwe było wykonanie pierwszego skoku-bicia. Ruchów powinno być jak najmniej; może ich być mniej niż bić, ponieważ dwa kolejne bicia (lub więcej) wykonane tym samym pionkiem stanowią jeden ruch.

Komentarze
Proponuję następującą wersję samotnika:
Plansza jest nieskończona, każde pole identyfikujemy przez parę liczb całkowitych (x, y). W sytuacji początkowej piony znajdują się na wszystkich polach z niedodatnią współrzędną y, tzn. y >= 0.
Zadanie:
Należy postawić piona na dowolnym polu o jak największej współrzędnej y.
Dla y=1 wystarczy jeden ruch. Dla y=2 wystarczą 4 ruchy. A ile ruchów (jakich?) potrzeba dla y=3, 4, 5, … A może w ogóle nie da się tego zrobić?
Uściślając przykład: ostatni ruch to musi być 2-10 i wtedy na polu 10 zostaje ten ostatni pionek.
Poprawione
mp
Przeniesienia jednego pionka na puste pole:
1-6
kolejne posunięcia:
1. 5-7
2. 13-5
3. 8-6
4. 5-7
5. 16-8
6. 4-12
7. 14-16 16-8 8-6
siódmy ruch to „combo” stąd taki zapis.
Ruchów może być 6.
mp
Najmniejsza liczba ruchów to 6 a poniższe rozwiązanie jest jedynym z tą ilością ruchów.
Wstępne posunięcie:
4 -> 6
Liczba ruchów = 6
5 -> 7
8 -> 6
13 -> 5
1 -> 9
15 -> 13
13 -> 5
5 -> 7
16 -> 8
8 -> 6
Jeśli ktoś jest zainteresowany to kod programu znajdzie na
https://github.com/Jacwing/SamotnikMini (współrzędna (0,0) to lewy górny róg).
@miodziu (wpis numer 191553)
Według mojej rachuby dla y=2 wystarczą 3 ruchy, dla y=3 starczy 7 ruchów, a dla y=4 potrzeba wiele ruchów (ale nie zapisałem ile i jak to zrobiłem).
Dla y=5 gołym okiem widać, że się nie da 🙂 bo przestrzeń między uciekającym pionem a pozostałymi rośnie geometrycznie, tylko jak to ująć ?
Bardzo prosto i globalnie pokazał to Karol Pokorski w marcowej Delcie z 2014 roku. Polecam wszystkim ten artykuł !!!!!!!
Aha, pierwszy raz widziałem to zadanie w starej angielskiej książce pożyczonej z British Council w W-wie w połowie lat 80-tych ale zupełnie nie pamiętam jakie tam było rozwiązanie, chociaż równanie x^2 + x = 1 występowało tak jak w/w artykule z Delty 🙂
@ miodziu + Spytko z Melsztyna
Riserczując zagadnienie napotkałem:
http://www.chiark.greenend.org.uk/~sgtatham/solarmy/
Zdecydowałem jednak o nie zagłębianiu się w tych żołnierzach Conwaya.
@Spytko z Melsztyna, @apartado
Mój wpis oczywiście był zainspirowany wymienionym artykułem w Delcie: http://www.deltami.edu.pl/temat/matematyka/gry_zagadki_paradoksy/2014/02/27/Nieskonczony_samotnik/
Wpis pisałem na szybko z głowy, dlatego pojawiły się w nim dwa drobne błędy:
1. Początkowa konfiguracja zawiera piony na polach o niedodatniej współrzędnej y, tzn. 0 >= y (a nie błędne „y >= 0”).
2. Dla y=2 wystarczą 3 ruchy. Podczas pisania wpisu nie zauważyłem tego rozwiązania, choć mimo wszystko napisałem prawdę, bo 4 ruchy również wystarczą 🙂