Minus trzy
W mailach, jakie otrzymuję od rozwiązujących zadania zamieszczone w Omnibusach, najczęściej pojawia się oczywiście to, co najbardziej konkretne, czyli uwagi dotyczące poszczególnych zadań, a zwłaszcza niedoróbek. „Niedoróbka” lub „usterka” jest właściwym słowem, bo zwykle chodzi o to, że jakaś łamigłówka ma więcej niż jedno podane rozwiązanie. W pierwszym tegorocznym, czyli ogólnie dziesiątym Omnibusie, jak dotąd czytelnicy odkryli jeden feler: kilka rozwiązań ma zadanie „Okrągły stół”. Ile? – to pytanie do wszystkich, którzy wakacyjnym Omnibusem dysponują i zmierzą się z zawiłościami informacji podanych na stronie 4.
Muszę też wspomnieć o skromnym gronie wnikliwych osób, które bardzo skrupulatnie rozwiązują, wręcz analizują wszystkie zadania i informują mnie o najmniejszych potknięciach. W tym gronie wyróżnia się Pani Kamila, która nadsyła pełną, drobiazgową „erratę” ze sporym, bo ponadrocznym opóźnieniem. Postanowiłem w związku z tym przypomnieć małe zadanie liczbowe z jednego z poprzednich Omnibusów, którego dodatkowe rozwiązanie odkryła jako jedyna Pani Kamila.
Z błędnej równości należy usunąć trzy znaki (z jednej lub obu stron znaku równości) tak, aby była poprawna. Znakami są liczby i znaki działań. Powstały po usunięciu znaków „luz” w działaniu jest likwidowany. Dostawianie nawiasów wykluczamy.
Ile jest rozwiązań i jak wyglądają poprawne równości?
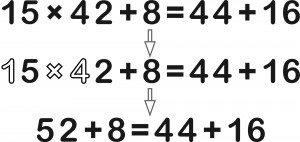

Komentarze
Ręcznie znalazłem 3 rozwiązania i jeśli się nie pomyliłem, to innych rozwiązań nie ma:
15+2 = 21-28/7 …= 17
212 = 216-28/7 …= 212
2*152 = 2128/7 …= 304
1)2×152=2128:7
2) 212=216-28:7
3) 15+2=21-28:7
Są trzy rozwiązania:
15+2=21-28:7=17
212=216-28:7=212
2*152=2128:7=304
15+2=21-28:7
212=216-28:7
2×152=2128:7
Mam póki co dwa:
15+2=21-28:7
2×152=2128:7
Trzy rozwiązania:
212 = 216-28:7
2×152 = 2128:7
15+2=21-28:7
Pozdrawiam,
Wydaje mi się, że w zadaniu „Okrągły stół” jest osiem rozwiązań.
212 =216-28/7, ale to coś podejrzanie łatwe rozwiązanie.
2×152=2128/7 – to rozwiązanie jest ciekawsze
Poza konkursem – rozwiązanie z usunięciem tylko dwóch znaków
2×5+2=16-28:7
Omnibus wakacyjny. Część 12.
Yin-yang (str.30).
W ostatnim (największym) diagramie jest więcej niż jedno rozwiązanie.
W wyniku powyższego, można postawić pytanie:
Co zrobić, najlepiej w sposób minimalistyczny, aby odpowiedź była jedna (np. taka jak w rozwiązaniu zamieszczonym na końcu Omnibusa)?
Najprostsza i ogólna odpowiedź: dostawić gdzieś jeden krzyżyk lub jedno kółko.
mp
Zadanie w Omnibusie ma 67 różnych rozwiązań. Aby było jedno rozwiązanie należy dodać co najmniej dwa znaki . Jeżli dodamy dwa X (zastąpione literą C aby uwidocznić) wtedy otrzymamy rozwiązanie z Omnibusa.
>>>>>>>>X>
>>>>>OX>>>
>>>O>X>>>>
>O>>>>>O>>
>>>O>C>>>>
>>>>>>>>X>
>>>>>CX>>>
>>>>O>>XX>
>>OO>>>>>>
>O>>>>>>>>
Można dodać też O i X (litery V i C)
>>>>>>>>X>
>>>>>OX>>>
>>>O>X>>>>
>O>>>>>O>>
>>>O>C>>>>
>>>>V>>>X>
>>>>>>X>>>
>>>>O>>XX>
>>OO>>>>>>
>O>>>>>>>>
Dodanie tylko jednego znaku (litera V w drugim rozwiązaniu) spowoduje, że zadanie będzie miało 4 różne rozwiązania.
Moim zdaniem wystarczy jeden znak, zjedzony przez chochlika 😉
Chodzi o krzyżyk umieszczony w centralnym kwadracie 2×2 na polu prawym górnym.
mp
Postać diagramu po dodaniu X (C)
>>>>>>>>X>
>>>>>OX>>>
>>>O>X>>>>
>O>>>>>O>>
>>>O>C>>>>
>>>>>>>>X>
>>>>>>X>>>
>>>>O>>XX>
>>OO>>>>>>
>O>>>>>>>>
Jeżeli dodamy wskazany X (C) to zadanie ma 10 rozwiązań
OOOOOOOXXX
OXXXXOXXOX
OXOOXXXOOX
OOOXXOOOXX
OXOOXXXOOX
OXXOOOOOXX
OOXXXXXOOX
OXXOOOXXXX
OXOOXOOOOX
OOOXXXXXXX
OOOOOOOXXX
OXXXXOXXOX
OXOOXXXOOX
OOOXXOOOXX
OXOOXXXOOX
OXXOXOOOXX
OOXXXOXOOX
OXXOOOXXXX
OXOOXOOOOX
OOOXXXXXXX
OOOOOOOXXX
OXXXXOXXOX
OXOOXXXOOX
OOOXXOOOXX
OXOOXXXOOX
OXOXXOOOXX
OXOXOOXOOX
OXXXOXXXXX
OXOOOOOOOX
OOOXXXXXXX
OOOOOOOXXX
OXXXXOXXOX
OXOOXXXOOX
OOOXXOOOXX
OXOOXXXOOX
OXOXXOOOXX
OXXXOOXOOX
OXOXOXXXXX
OXOOOOOOOX
OOOXXXXXXX
OOOOOOOXXX
OXXXXOXXOX
OXOOXXXOOX
OOOXXOOOXX
OXOOXXXOOX
OXXXXOOOXX
OXOOOOXOOX
OXXXOXXXXX
OXOOOOOOOX
OOOXXXXXXX
OOOOOOOXXX
OXXXXOXXOX
OXOOXXXOOX
OOOXXOOOXX
OXOOXXXOOX
OXXXXOOOXX
OOXOOOXOOX
OXXXOXXXXX
OXOOOOOOOX
OOOXXXXXXX
OOOOOOOXXX
OXXXXOXXOX
OXOOXXXOOX
OOOXXOOOXX
OXOOXXXOOX
OXXXXOOOXX
OOOXOOXOOX
OXXXOXXXXX
OXOOOOOOOX
OOOXXXXXXX
OOOOOOOXXX
OXXXXOXXOX
OXOOXXXOOX
OOOXXOOOXX
OXOOXXXOOX
OXXXXOOOXX
OXOXOOXOOX
OXOXOXXXXX
OXOOOOOOOX
OOOXXXXXXX
OOOOOOOXXX
OXXXXOXXOX
OXOOXXXOOX
OOOXXOOOXX
OXOOXXXOOX
OXXXXOOOXX
OXOOXOXOOX
OXXOOOXXXX
OXOOXOOOOX
OOOXXXXXXX
OOOOOOOXXX
OXXXXOXXOX
OXOOXXXOOX
OOOXXOOOXX
OXOOXXXOOX
OXXXXOOOXX
OOXOXOXOOX
OXXOOOXXXX
OXOOXOOOOX
OOOXXXXXXX
Po umieszczeniu krzyżyka w centralnym kwadracie 2×2 na polu prawym górnym nadal będzie więcej niż jedno rozwiązanie.
Istotnie. Jak wykazał Antyp, rozwiązań jest wówczas 10, czyli nawet gdyby chochlik nie spłatał figla, usterka by pozostała. Mea kulpa – zadanie przerosło autora.
mp
Ponieważ strzałki z aktualnego wpisu nie za bardzo mnie pociągają, sięgnąłem do letniego Omnibusa z 2016 roku. Przeglądając go trafiłem na stronę 52 i łamigłówkę Złotobranie. Wcześniej rozwiązałem tylko zadanie a. Jakież było moje zdziwienie gdy po rozwiązaniu zadania b zerknąłem na koniec i zobaczyłem, że ma jeszcze jedno rozwiązanie. Przyłożyłem się bardziej i znalazłem trzecie rozwiązanie tego zadania.
1 2 12 13 6 5 14
. 3 . . . 4 .
. . 11 10 . 9 .
. . . . 7 8 .
Wynik śledztwa w stosunku do pozostałych zadań poniżej.
Zad. e
. . 5 1 6 . . .
. . . 2 . . . .
. 8 4 3 7 . . .
16 . 15 14 13 12 . .
17 9 . . 10 11 18 19
. . 6 1 5 . . .
. . . 2 . . . .
. 8 7 3 4 . . .
16 . 15 14 13 12 . .
17 9 . . 10 11 18 19
. . 7 1 8 . . .
. . . 2 . . . .
. 10 6 3 9 . . .
16 . 5 4 15 14 . .
17 11 . . 12 13 18 19
. . 8 1 7 . . .
. . . 2 . . . .
. 10 9 3 6 . . .
16 . 15 4 5 14 . .
17 11 . . 12 13 18 19
. . 14 1 13 . . .
. . . 2 . . . .
. 10 11 3 12 . . .
16 . 15 4 5 6 . .
17 9 . . 8 7 18 19
Zad. f
. . 12 13 .
. 6 . . 5
. 3 . . 4
1 2 11 10 9
. 7 . . 8
. . 15 14 .
. . 15 14 .
. 6 . . 5
. 3 . . 4
1 2 11 10 9
. 7 . . 8
. . 12 13 .
. . 12 11 .
. 6 . . 5
. 3 . . 4
1 2 13 10 9
. 7 . . 8
. . 14 15 .
. . 14 15 .
. 6 . . 5
. 3 . . 4
1 2 13 10 9
. 7 . . 8
. . 12 11 .
Zad. g
1 . . 2 . . . .
. 10 . . 11 . 12 .
. . 16 3 4 5 . 17
. . 15 . 14 . 13 .
. 9 8 . 7 6 . .
1 . . 2 . . . .
. 12 . . 11 . 10 .
. . 16 3 4 5 . 17
. . 15 . 8 . 9 .
. 13 14 . 7 6 . .
Zad. h
. 1 . . . . . .
3 2 13 14 15 . . .
4 5 12 . . 11 . .
. 6 . 7 . . 8 .
. . . . 16 . . 17
. . . . . 10 9 18
. 1 . . . . . .
12 2 13 14 15 . . .
11 3 10 . . 9 . .
. 4 . 5 . . 6 .
. . . . 16 . . 17
. . . . . 8 7 18
. 1 . . . . . .
3 2 15 14 13 . . .
4 5 16 . . 17 . .
. 6 . 7 . . 8 .
. . . . 12 . . 11
. . . . . 18 9 10
. 1 . . . . . .
15 2 3 14 13 . . .
16 5 4 . . 17 . .
. 6 . 7 . . 8 .
. . . . 12 . . 11
. . . . . 18 9 10
. 1 . . . . . .
13 2 3 14 15 . . .
12 5 4 . . 11 . .
. 6 . 7 . . 8 .
. . . . 16 . . 17
. . . . . 10 9 18
. 1 . . . . . .
14 2 13 12 11 . . .
15 3 16 . . 17 . .
. 4 . 5 . . 6 .
. . . . 10 . . 9
. . . . . 18 7 8
. 1 . . . . . .
14 2 13 12 11 . . .
15 3 16 . . 17 . .
. 4 . 5 . . 6 .
. . . . 10 . . 9
. . . . . 18 7 8
. 1 . . . . . .
13 2 3 14 15 . . .
12 11 4 . . 5 . .
. 10 . 9 . . 8 .
. . . . 16 . . 17
. . . . . 6 7 18
Aby zadanie (h) miało jednoznaczne rozwiązanie 1-ką należałoby
oznaczyć inne pola (są 2 rozwiązania).
. 18 . . . . . .
16 17 6 7 8 . . .
15 4 5 . . 14 . .
. 3 . 2 . . 1 .
. . . . 9 . . 10
. . . . . 13 12 11
. 18 . . . . . .
16 17 7 8 9 . . .
15 5 6 . . 14 . .
. 4 . 3 . . 2 .
. . . . 10 . . 11
. . . . . 13 1 12