A to feler

6 maja 2016
Marek Penszko

Nie lubię popełniać błędów (kto lubi?), ale nie mam oporów, aby się do nich przyznawać. Nie podzielam też stwierdzenia o uczeniu się na błędach, zwłaszcza że błędy bywają różne. Są takie, które popełniamy regularnie, niekoniecznie z powodu roztargnienia lub gapiostwa.

Wracając do łamigłówek, błąd może być okazją do dodatkowej zagadki przy okazji powtórzenia zadania, w którym został popełniony, co niniejszym postanowiłem uczynić. Błąd jest w tym przypadku szczególny, nazwałbym go raczej drobnym felerem, a dotyczy zadania zamieszczonego w marcowym Świecie nauki.

Atf_1

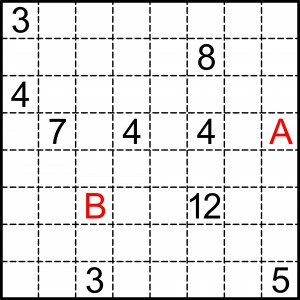
Diagram na rysunku należy podzielić wzdłuż linii przerywanych na 11 prostokątów tak, aby w każdym znalazła się jedna liczba lub litera. Każda liczba oznacza pole (liczbę kratek) lub połowę obwodu prostokąta, w którym się znajdzie (jednostką długości jest bok kratki). Dotyczy to także dwóch liczb zastąpionych literami A i B. Jaką liczbę zastępuje każda z liter, jeśli jedna z odpowiadających im liczb jest dwukrotnie większa od drugiej?
I wspomniana dodatkowa zagadka: na czym polega usterka tego zadania?

Kom