Po czwarte
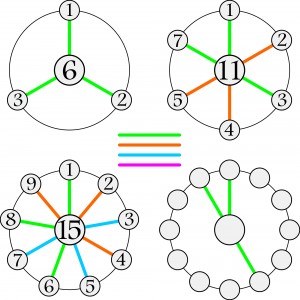
Łamigłówka á la Mensa, tylko trochę bardziej zakręcona, czyli należy dokończyć czwarty z „rozwojowej” serii obrazków – wpisać odpowiednie liczby w kółka i dorysować łączące je linie we właściwych kolorach – poza zielonymi, które są już na właściwym miejscu. „Rozwój” figury, która na dalszych etapach przypomina diabelski młyn, jest oczywiście zgodny z jakimiś zasadami, które wypadałoby rozszyfrować.
Rozwiązania obrazkowe mile widziane. Opisowe również.

Komentarze
Czy rozwiązanie może wyglądać tak?
http://pokazywarka.pl/1k0sg9/
Moim zdaniem nie, ale może da się to jakoś uzasadnić, tzn. czy może Pani podać jakieś reguły łączące obrazki?
mp
Trzy kółka wskazane liniami jednego koloru zawierają liczby dające sumę widniejącą w środkowym kółku. Liczby na okręgu ułożone są rosnąco.
To właściwie wszystkie reguły, jakie mi przyświecały. Rozumiem, że tej najważniejszej nie zauważyłam…
No tak, troszkę za mało, tzn. można uściślić reguły.
mp
Kółek jest 12 tak jak w zegarze.
Suma wszystkich liczb od 1 do 12 to 78 i jeśli mamy je podzielić na cztery sumy po 3 to by nie wyszło całkowicie. Żeby poprawić sumę do podzielności przez 4 można np. dwa ostatnie elementy podnieść o 1. Taki nowy zegar będzie miał liczby:
1,2,3,4,5,6,7,8,9,10,12,13, których suma to 80.
Można to podzielić na cztery grupy po trzy liczby z sumą 20.
Czyli na środku jest 20.
zielone linie: 1,6,13
brązowe linie: 2,8,10
niebieskie linie: 3,5,12
różowe linie: 4,7,9
Czy tak będzie OK?
Tip-top!
mp
Warunkiem dodatkowym musi być suma liczb wynosząca jak najmniej.
Moim typem są 4 trójki liczbo łącznej sumie 80=4*20
(78=suma(1..12) nie dzieli się przez 4):
1,6,13
2,8,10
3,5,12
4,7,9
W rozwiązaniu OlaGM sumowanie jakoś nie wyszło…
Trzecia reguła: szprychy jednego koloru powinny tworzyć takie same układy (dopuszczamy przewracanie na drugi bok)
1+6+13 = 2+8+10 = 3+5+12 = 4+7+9 = 20
Rozwiązanie: http://i.imgur.com/MdccCmr.jpg
Zasady:
1) W każdej kolejnej figurze o trzy pola więcej na okręgu i jeden dodatkowy kolor.
2) Liczby na okręgu rosnąco ze wskazówkami zegara.
3) Po trzy kreski danego koloru z pól na okręgu do środkowego pola, suma liczb z trzech pól na okręgu równa liczbie w środku.
4) Liczba w środku możliwie najmniejsza.
Ola,
Twoje brązowe się nie chcą zsumować do 20.
propozycja rozwiązania: http://bankfotek.pl/view/1905601
Suma trzech liczb połączonych odcinkami o takim samym kolorze wynosi 20. W każdym sektorze (składającym się z 4 cyfr) zaczynając od kółka z 1 występują wszystkie cztery kolory.
http://pokazywarka.pl/z4r9s2/
Liczby na okręgu muszą być różne, ułożone rosnąco i możliwie jak najmniejsze. Połączone jednym kolorem linii sumują się do liczby w środku. Kolorów ma być 4, linii w każdym kolorze po 3.
Dla tych warunków minimalna suma to 80, co daje w środku liczbę 20. Kolejne liczby na okręgu (zaczynając od tej nad środkową) to 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 12 i 13. Połączone zielonym kolorem są liczby 1, 6 i 13, pozostałe trójki to 2, 8 i 10; 3, 5 i 12 oraz 4, 7 i 9.
Podobnie jak Spytko byłem przekonany, że dodatkową regułą jest podobieństwo układów. W końcu szansa, że przypadkowo trafimy trzecim kole na taki zestaw wynosi 3/280, a w drugim 1/10. Dodatkowo układ w czwartym kole pozwalał zestawić resztę szprych tylko na dwa sposoby:
1,6,12; 2,7,8; 3,4,9; 5,10,11
lub
1,6,12; 2,7,8; 3,9,10; 4,5,11
(liczby oznaczają pozycję na kole, nie wartości małych kółek)
W tym momencie utknąłem, nie udało mi się znaleźć zestawu liczb sumującego się do jednej liczby (pewnie jest takich wiele, ale oczywiście chodziło o najmniejszą sumę przy zachowaniu kolejności na kole).