Zerówka
W komentarzach do poprzedniego wpisu sypnęło kwadratami magicznymi do Melancholii II. Nie przypuszczałem, że pojawi ich się aż tyle. Dziękuję w imieniu grafika, który będzie miał w czym wybierać.
Postanowiłem pozostać przy kwadratach liczbowych, ale nieco innych. Zacznę od sformułowania zadania, a potem wyłuszczę co wytłuszczę.
Z dziewięciu różnych cyfr należy utworzyć kwadrat różnicowy, który będzie można wyzerować w sześciu ruchach.
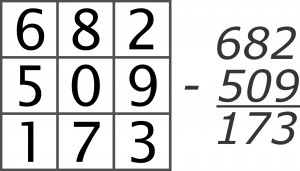
Kwadrat różnicowy jest diagramem złożonym z 9 pól (3×3), w które wpisano cyfry w taki sposób, że w trzech rzędach powstały 3-cyfrowe liczby tworzące poprawne odejmowanie. Przykład z dziewięcioma różnymi cyframi:
Wyzerować kwadrat różnicowy oznacza doprowadzić w określonej liczbie ruchów do zmiany wszystkich cyfr w zera, czyli:
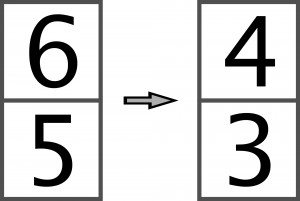
Ruch polega na zmniejszeniu cyfr znajdujących się w dwu sąsiednich polach (mających wspólny bok) o taką samą wartość.
Przykład (sąsiednie liczby maleją o 2):
I wszystko (mam nadzieję) jest jasne.
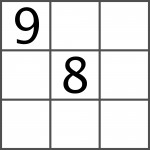
Na dobry początek dwie cyfry w kwadracie różnicowym są ujawnione. Pozostaje wpisać siedem pozostałych.
Dla wytrwałych programistów: kto bez „dobrego początku” znajdzie drugie (więcej nie ma) rozwiązanie tego zadania?


Komentarze
Panie Marku, z tymi „wytrwałymi programistami” to bym uważał… W tym wypadku, to nawet początkujący programista powinien sobie poradzić w 5 minut, więc określenie „wytrwały” jest mocno przesadzone 😉
Tak sobie zapółżartowałem
mp
Oto oba rozwiązania:
940 – 687 = 253
450 – 263 = 187
Zakładając dodatkowo, że liczba trzycyfrowa może rozpoczynać się od zera wiodącego, mamy kilka innych rozwiązań:
243-78=165
234-58=176
236-49=187
243-56=187
246-59=187
351-87=264
364-89=275
562-89=473
I muszę ze skruchą przyznać, że te 5 minut to była wielka przesada. Mnie pisanie programu zajęło jakieś 30-40 minut, a wykonanie programu ok. 3 minuty. Obiecuję więcej nie półżartować 🙂
Cyfry nie muszą być różne?
„Z dziewięciu różnych cyfr…” – czyli muszą.
mp
940
687
253
450
263
187
Jeśli nie pomyliłem się w obliczeniach 🙂 to żaden inny układ nie da się wyzerować w dowolnej liczbie ruchów.
Istotnie – liczba ruchów nie jest istotna :).
mp
940-687=253
940 500 000 000 000 000 000
687 687 187 110 000 000 000
253 253 253 253 253 033 000
Rozwiązania bez warunku 9-8 mieszczą się w 12 układach, które trzeba sprawdzić ręcznie:
940 568 372
940 578 362
940 657 283
940 687 253
750 289 461
750 489 261
920 736 184
920 786 134
640 289 351
640 389 251
630 478 152
720 586 134
Naprawdę istnieje drugie rozwiązanie?
1. cyfry składają się z 4 rożnych nieparzystych i 5 różnych parzystych cyfr
2. jeśli podzielimy planszę na pola czarne i białe jak szachownicę, suma cyfr na polach białych = suma cyfr na czarnych.
3. pierwsza cyfra żadnej liczby nie jest zerem
4. liczby spełniają równanie a – b = c
Mój komputer mówi, że tylko jeden układ cyfr spełnia powyższe warunki.
Drugie rozwiązanie znalazłem „na piechotę”. Czyżby triumf człowieka nad maszyną?
mp
450 010 000 000 000 000 000
263 263 253 033 000 000 000
187 187 187 187 187 077 000
Jeżeli dopuści się zero na cyfrze setek, to jest jeszcze 8 rozwiązań (nie sprawdzałem liczby ruchów do wyzerowania):
364 089 275
562 089 473
246 059 187
236 049 187
234 058 176
243 056 187
243 078 165
351 087 264
A co do „triumfu człowieka nad maszyną”, to zawsze jest to triumf człowieka nad człowiekiem.
Mój błąd był w pośpiesznym przypisaniu *kolejnych* liczb całkowitych *kolejnym* polom planszy w taki oto nietypowy sposób:
012
345
768
Proponuję następujące kwadraty:
9 5 4
6 8 3
2 7 1
oraz:
9 0 7
3 8 6
5 2 1
Te dwa kwadraty to
940
687
253
oraz
450
263
187
Aby je stworzyć należy zauważyć, że
1.suma cyfr użytych w kwadracie musi być parzysta (czyli nie można użyć cyfr od 1 do 9).
2.jeżeli potraktujemy kwadrat jak szachownicę to suma cyfr na polach białych jest równa sumie cyfr na polach czarnych.
3. każda z cyfr w polach narożnych i w polu środkowym musi być mniejsza bądź równa sumom cyfr w polach do niej przylegających bokiem.
Jeżeli pierwsza cyfra liczby może być równa zero to takich kwadratów jest więcej np:
246
059
187