Dwunasty kamień
Pięć kwadratów można połączyć bokami na 12 różnych sposobów, tworząc 12 figur całkowicie różnych (żadne dwie nie są względem siebie odbiciami lustrzanymi). Jeśli te figury „ożywić”, czyli nadać im formę płaskich kamieni albo chociaż wyciąć z kartonu, to powstanie komplet zwany pentominem, czyli jedna z najpopularniejszych w minionym półwieczu łamigłówek układanek. Modę na nią zapoczątkował artykuł Martina Gardnera zamieszczony na łamach Scientific American w 1957 roku. W rezultacie niedługo potem w sklepach z zabawkami w większości krajów pojawiły się pudełeczka z tuzinem drewnianych lub plastikowych wieloboków, a pentominowe łamigłówki zaczęły coraz częściej gościć w rozrywkowych działach czasopism, zwłaszcza popularnonaukowych.
Pentomino to evergreen – artykuły dotyczące tej układanki wciąż pojawiają się w różnych publikacjach, także stricte matematycznych. Dostrzeżono również jej walory edukacyjne, więc czasami uatrakcyjnia lekcje matematyki. W sieci jest mnóstwo stron poświęconych bezpośrednio pentominu, a także zagadnieniom lub grom, w których się pojawia. Problemów oraz konkretnych łamigłówek wymyślono setki i wciąż ich przybywa. Proponuję pogłówkować nad jedną z nich.
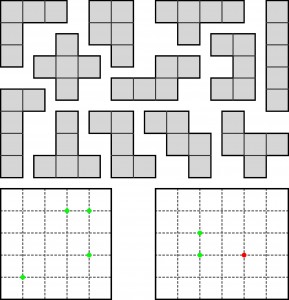
U góry jest komplet pentomina, u dołu – dwa prostokąty ułożone z 11 różnych kamieni. Należy oznaczyć granice między kamieniami, korzystając tylko z oznaczonych kropek. Zielone znajdują się w miejscach styku trzech kamieni, czerwona – w miejscu, gdzie stykają się rogami cztery kamienie. Żadna figura w prostokątach nie jest odbiciem lustrzanym figury na górnym rysunku.
Jako rozwiązanie końcowe wystarczy podać, którego kamienia brakuje w prostokątach.

Komentarze
http://www.gg.pl/dysk/mhefexKSdq5QmxefexKSZoc/dwunastykamien.png
Brakuje kamienia w kształcie litery W. Zakładanie konta aby opublikować komentarz mnie osobiście wkurza.
Mnie też, ale może są jakieś argumenty za.
m
czy wszystkie styki 3 i 4 kamieni zostały oznaczone kropkami czy niekoniecznie?
Tak, wszystkie.
mp
Są dwa rozwiązania.
W pierwszym nie ma kamienia w kształcie litery W
http://pokazywarka.pl/3j38py/
W drugim nie ma krzyża
http://pokazywarka.pl/1ug0yw/
Byłoby drugie, gdyby nie warunek zaczynający się od „Żadna figura…”.
mp
Rzeczywiście, a więc jest jedno rozwiązanie: bez kamienia W 🙂
Brakuje „W”
w rozwiązaniu brakuje kamienia prawego od prawej w dolnym rzędzie
http://bankfotek.pl/view/1832333
drugiego od prawej* miało być 🙂