Koniec łat
Ostatni kwadrat łaciński łaciaty jest dodatkowo łamigłówką indukcyjną, czyli na początku trzeba rozszyfrować zasady zabawy, wnioskując z przykładu. A przykład wygląda tak:
Dla nowicjuszy indukowanie może być trudne, ale jeśli zerknąć do bliźniaczej łamigłówki z poprzedniego wpisu, będzie zapewne znacznie prościej. Po odgadnięciu instrukcji obsługi proponuję z niej skorzystać, czyli pogimnastykować szare komórki nad poniższym zadaniem.
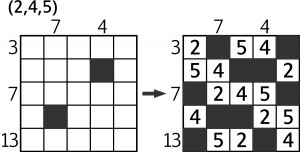
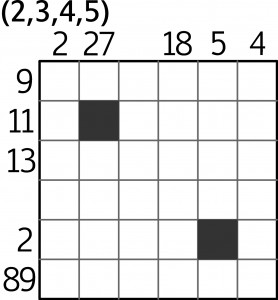

Komentarze
Indukcja indukcją, ale pewne rzeczy nie są jasne.
Pytanie 1:
Który z powyższych ciągów mógłby być górnym wierszem rozwiązania:
45X32X
32X45X
Pierwszy, drugi, czy oba?
Pytanie 2:
Czy w przedostatnim wierszu może stać coś takiego:
X345X2 ?
Czy też możemy przyjąć w obu kwestiach dowolne założenia?
Rozumiem, że pytanie „który mógłby być?” oznacza, że spełniałby warunek związany z liczbą przy brzegu diagramu.
Jeśli tak, to (p)odpowiadam:
– pytanie 1: 32X45X
– pytanie 2: nie
mp
x54x23
4x253x
x234x5
34xx52
53x2x4
2x534x
Teraz wszystko jasne. Rano „wyindukowałem”, że wskazówki z boku planszy oznaczają podzielniki najdłuższych liczb w zapisie dziesiętnym w danym wierszu/kolumnie, a chodziło o podzielniki liczb miedzy zaczernionymi kratkami.
Treść zadania brzmi tak:
W każdym rzędzie diagramu (pionowym i poziomym) należy zaczernić dokładnie dwa pola oraz umieścić cyfry widoczne przy diagramie (każdą dokładnie jeden raz) tak, aby liczba podana przy brzegu diagramu przy danym rzędzie była dzielnikiem liczby utworzonej w danym rzędzie pomiędzy polami zaczernionymi.
Rozwiązanie zadania:
#54#23
4#253#
#234#5
34##52
53#2#4
2#534#
PS. Bardzo fajne zadanie.
PPS. Znowu obyło się bez komputera 🙂
X54X23
4X253X
X234X5
34XX52
53X2X4
2X534X
Komputer przy rozwiązywaniu nie był potrzebny, ale kalkulator mógł się przydać (chyba, że ktoś zna na pamięć wszystkie trzycyfrowe wielokrotności 89)
x54x23
4x253x
x234x5
34xx52
53x2x4
2x534x
Następująca reguła: Liczba stojąca przy rzędzie to największy czynnik pierwszy jaki można uzyskać z rozkładu wszystkich liczb w rzędzie – sypie się „tylko” na czwórce (która nie jest liczbą pierwszą 🙂 ). Czy jestem blisko czy zupełnie inny kierunek ???
Rozwiązanie znalazłem jedno :
X54X23
4X253X
X234X5
34XX52
53X2X4
2X534X
a reguła dodatkowa to oczywiście podzielność liczb odciętych czarnymi polami przez liczbę podaną na skraju diagramu
dziękuję i pozdrawiam
AC