Jednym ciachem
Różnica między zadaniem matematycznym a łamigłówką matematyczną jest płynna, ale w poprzednim wpisie zdecydowanie było zadanie – tak dla odmiany. Tym razem też będzie dla odmiany, choć może nie tak zdecydowanie. Kontynuujemy bliski mi (ze względu na wykształcenie) temat formatów drukarskich.
Zasada tworzenia ciągu formatów A, B i C jest prosta, sprytna i gospodarna, bo bez strat. O taka:
Wystarczy jeden ciach na pół i z większego formatu a×b powstaje mniejszy format b×a/2, a co najistotniejsze – zachowane zostają proporcje, czyli a/b=b/(a/2). Aby wszystko grało, należy tylko obliczyć proporcje formatu wyjściowego, czyli zerowego i przyjąć konkretne wymiary. Wymiary wyjściowe bywają różne, ale proporcje stałe:
a/b = sqrt2 = 1,414…
Gdybyśmy zażyczyli sobie, by początkowy i każdy kolejny format był złotym prostokątem, czyli aby:
a/b = fi = (1+sqrt5)/2 = 1,618…
oraz gdybyśmy pozostali przy jednym cięciu, wówczas straty byłyby ogromne: od każdego formatu należałoby odcinać kwadrat, tworząc format oczko mniejszy.
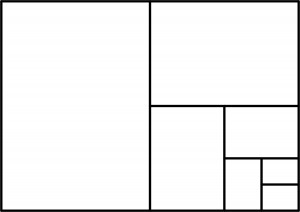
Proszę obliczyć wartość a/b (z dokładnością do trzech cyfr po przecinku) dla ciągu formatów, powstających w następujący sposób: z brzegu każdego formatu jednym cięciem usuwane jest domino (prostokąt, którego jeden bok jest dwukrotnie dłuższy od drugiego).

Komentarze
W tym przypadku jest do ułożenia proporcja
a/b=b/(a-1/2*b)
a i b to długości boków formatu
po przekształceniach
a/b=1/(a/b-1/2)
x=a/b
x=1/(x-1/2)
Rozwiązanie tego równania daje wynik
(1+sqrt(17))/4 to jest około 1,2808
a/b=b/(a-b/2) skąd a/b=(1+sqrt(17))/4 co daje w przybliżeniu 1,2807764…
a/b = (b-a/2)/a, skąd a/b = 0.78…
Teraz poprosimy coś trudniejszego.
Dobrze, ale odwrotnie (chodzi o 0.78…)
mp
Wydaje się, że wyjściowy format także powinien być „dominem”, a zatem a/b (tj. szerokość do wysokości) = 2,000 i wg założenia dla każdego odciętego formatu zachodzi ten sam związek.
Tym razem trzeba rozwiązać równanie: x = 1/(x-1/2), gdzie x to szukany stosunek dłuższego boku do krótszego. Rozwiązaniem jest x = (1+pierwiatek(17))/4, czyli ok. 1,280776
W odróżnieniu od poprzedniego, w tym zadaniu mamy równanie kwadratowe, wyglądające prosto, ale nie daje się w rozwiązaniu uniknąć pierwiastka kwadratowego z 17: a = (1 + sqrt17)/4, co daje w przybliżeniu 1,281. Drugi pierwiastek pomijamy, bo jest liczbą ujemną.
Jak się okazało, źle zrozumiałem zadanie. Zatem wariant nr 2: Założenie jest takie, że po odcięciu pewnego paska (o długości równej dwóm jego szerokościom) większa część arkusza stanowi „domino”. Z mniejszej części znowu mogę odciąć część o długości równej dwóm jego szerokościom i otrzymuję kolejne „domino”. W ten sposób można postępować w nieskończoność.
Dla takiego założenia długość wyjściowego arkusza (o szerokości A), wynosi:
A*(SQR(2)+1)=2,4142*A
@Jędrek
Masz prostokąt a na b, powiedzmy że a to ten dłuższy bok, i te boki są w jakimś tam stosunku a:b. Kawałek odcinasz równolegle do krótszego boku i to co zostanie ma mieć stosunek boków równy tyle samo, z tym że teraz to ten b jest w roli tamtego a.
Ale do pomyślenia jest także drugie rozwiązanie: prostokąt jest długaśny i odcinamy fragment, którego krótszym bokiem jest bok b, a dłuższym 2*b, bo nie jest powiedziane, jak to domino ma być ułożone. Wtedy rozwiązaniem jest 1+sqrt2, czyli 2,414. Teraz patrzę, że Jędrek to już podał, nie wiem czemu został uwolniony 🙂
Wyjątkowo nie dlatego, że rozwiązanie jest błędne (sorry Jędrku). Raczej przeciwnie.
mp
~1,281
Są dwa rozwiązania. Jedno zostało już uwolnione (1+sqrt(2)) = 2,414213562…, drugie to (1+sqrt(17))/4 = 1,28077640…
Otóż to. Znalezienie jednego rozwiązania jest „szkolne”, wpadnięcie na to, że są dwa – „łamigłówkowe”.
mp
Przyjmujemy a>b.
Mamy więc 2 rozwiązania:
Odcinamy małe domino („naturalne”), a/b=b/(a-b/2), a/b=(1+sqrt(17))/4
Odcinamy duże domino, („nienaturalne” brawa dla Jędrka 🙂 ), a/b=b/(a-2b), a/b=1+sqrt(2)