Macki z zagadką
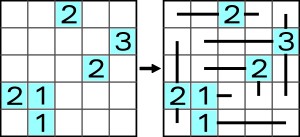
Jeśli zaczniemy rozwiązywać poniższe macki zgodnie z „klasycznymi” regułami
to okaże się, ze rozwiązania są dwa:
Aby było jedno, wystarczyłoby np. jedną z trójek przy brzegu przenieść do rogu. Można także zmienić wartości prawie wszystkich cyfr bez ich przenoszenia, np. tak:
Tylko że teraz są to już inne macki. Jakie są ich zasady? – oto zagadka indukcyjna do rozgryzienia na podstawie powyższego przykładu z rozwiązaniem. A po rozszyfrowaniu zasad należy z nich skorzystać przy rozwiązywaniu zadania:
W rozwiązaniu wystarczy podać, ilu pól sięgają mackami dwójki.




Komentarze
Dwójki sięgają 27 pól.
Cyfry w polach określają w ilu kierunkach wychodzą macki.
Macki wychodzące z tego samego pola muszą mieć różną długość (poza tym warunkiem macki mogą mieć dowolną długość, oczywiście muszą dosięgać każdego pola).
Przyjemne zadanie 🙂
Liczba oznacza
-ile w sumie pól zajmują macki, lub
-ile odcinków różnej długości z kratki z nią wychodzi
odp. 24
Zasady macek:
1. Od każdego pola z liczbą wychodzi tyle macek, ile wynosi wartość liczby.
2. Każda z macek wychodzących z tego samego pola, musi mieć długość różną od pozostałych.
http://pokazywarka.pl/1g5rd2/
Cyfra oznacza ilość macek wychodzących z pola; macki muszą być różnej długości.
27 pól:
3x 1+2
3x 2+4
Ciekawy, choć niezbyt trudny problem. Przesunąć wszystkie liczby w pierwszym diagramie (1,3,3,3,3,6 – bez zmiany wartości), każdą tylko o jedno pole (poziomo, pionowo lub ukośnie), tak aby macki miały jedno rozwiązanie.
Jeśli dobrze zrozumiałem reguły to przykład ma conajmniej 4 rozwiązania?
Mam na myśli narożniki lewy-górny i prawy-dolny.
… nawet 6…
Hmm, zadanie wydaje się mieć bardzo wiele rozwiązań.
Liczba w polach oznacza w ilu kierunkach wysyłane są macki.
Macki dwójek dosięgają do 26 pól
Nie wiem, czy spelnilem wszystkie warunki zadania, ale na pewno spelniony jest ten, ze od kazdej liczby wychodzi odpowiednia liczba odcinkow.
http://s1.pokazywarka.pl/i/2063204/486785/macki-z-zagadka.jpg
jb_filip: wydaje mi się, że macki nie mogą stykać się ze sobą głowami w tym samym kierunku, inaczej mówiąc: koniec macki musi ‚walić’ łbem w bok innej macki (lub w kratkę z liczbą). Inaczej zmienna długość obu macek stykających się ‚głowami’ generowałaby wiele więcej rozwiazań.
Czy istnieją jakieś strony z planszami „światowida” online? Albo chociaż do wydruku ?Mimo długich poszukiwań nie znalazłem żadnej (posługiwałem się w wyszukiwaniu zarówno nazwą japońską jak i alternatywnymi wersjami) Chciałbym zainteresować tą łamigłówką mojego 12-letniego syna.
Nie znam strony z większą liczbą takich zadań. Porcje 1-4 zadań trafiają się na japońskich stronach. Można je odszukać korzystając z nagłówka artykułu w japońskiej Wikipedii dotyczącego „światowidów”, czyli wall logic. Przykładowa strona z 4 zadaniami.
mp
Ciekawe, że jak korzystam z tych japońskich stron i tłumaczę to na polski, to lepiej to rozumiem jak najpierw przetłumacze na angielski. Od razu na polski jest niezrozumiałe 🙂