Bez cyfr
Liczby w diagramie mogą wysuwać macki (proste odcinki) w czterech kierunkach – w wierszach i kolumnach. Wartość każdej liczby oznacza, ilu w sumie pól może ona sięgnąć mackami. Macki powinny dotrzeć do wszystkich pustych pól, ale żadne dwie nie mogą sięgnąć tego samego pola.
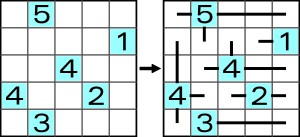
To tyle gwoli przypomnienia zasad łamigłówki zwanej mackami. I przykład:
Gdyby z diagramu przykładowego zadania usunąć jedną liczbę, to odtworzenie jej wartości byłoby trywialne, skoro suma liczb równa jest liczbie wolnych pól. A czy jednoznacznie dałoby się określić jej pozycję? Czasem tak, czasem nie. Na przykład piątka może być tylko w jednym polu, aby macki miały sens (jedno i tylko jedno rozwiązanie), ale jedynka w dwóch.
A gdyby usunąć kilka cyfr, oznaczając jednak miejsca, w których powinny się one znaleźć, to czy rekonstrukcja zadania i jego rozwiązanie mogłyby być jednoznaczne? Bez dodatkowych informacji nie. Usuńmy w ten sposób wszystkie cyfry z przykładowego zadania, a przy brzegu umieśćmy (jak w zadaniu z poprzedniego wpisu) możliwie najmniej liczb – każda z nich będzie sumą cyfr, które powinny znaleźć się w danym rzędzie lub kolumnie. Oczywiście należy to zrobić tak, aby na podstawie sum udało się jednoznacznie zrekonstruować macki, równocześnie je rozwiązując. Wydaje się, że mniej niż cztery liczby nie zapewnią jednoznaczności, przy czym przynajmniej dwie z nich będą „sumami” jednego składnika, np.:
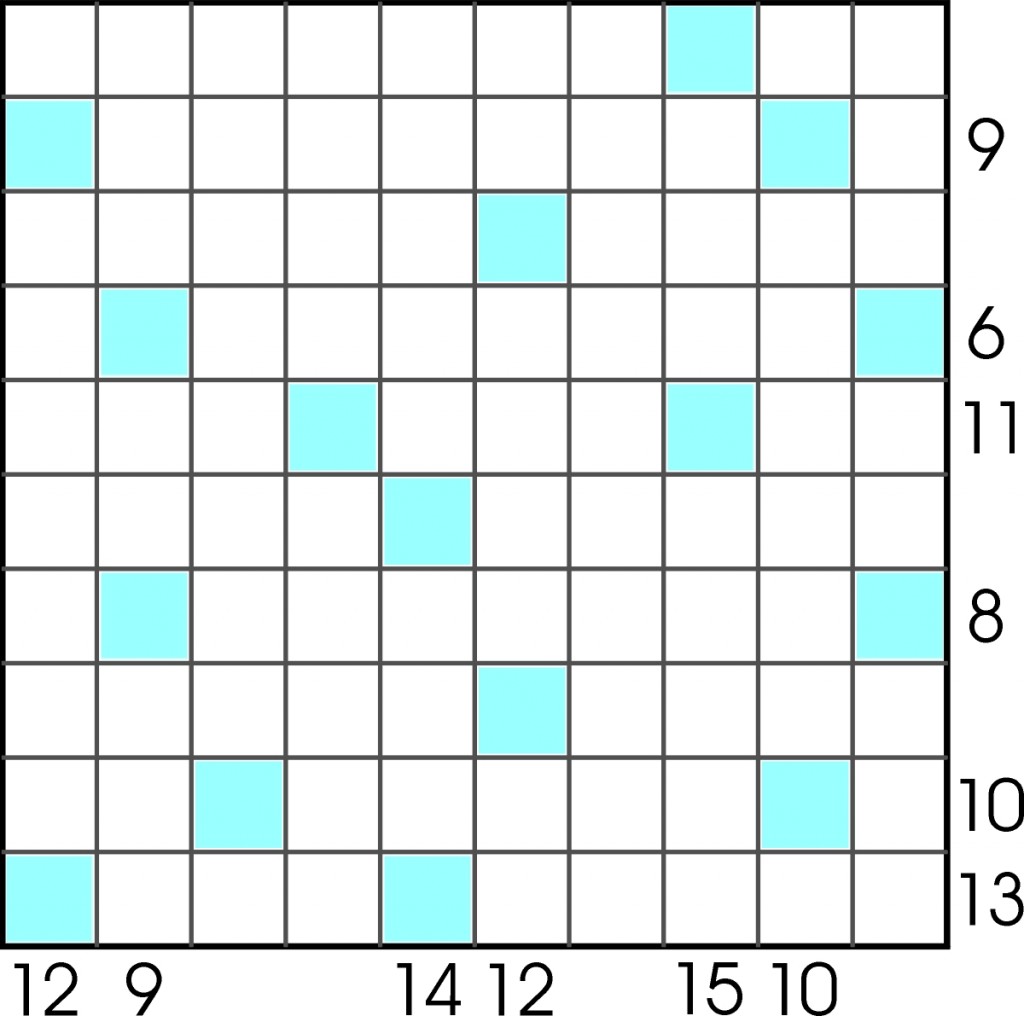
W poniższym zadaniu, opartym na takiej samej zasadzie, wszystkie sumy są jak należy – dwuskładnikowe.
Gwoli ścisłości – w diagramie brak 16 liczb jednocyfrowych większych od zera.
W rozwiązaniu wystarczy podać sumę liczb sięgających mackami dziewięciu pustych pól na przekątnej łączącej lewy dolny róg z prawym górnym.
I jeszcze na wszelki wypadek „ostrzeżenie”: zadanie jest bardzo trudne – tylko dla spostrzegawczych i cierpliwych orłów.


Komentarze
W przedostatnim diagramie byłoby lepiej dobrać inne sumy, bo te które są nie dają jednoznaczności rozwiązania.
Sumy liczb z dwóch przekątnych z zadania dla spostrzegawczych: (59,39).
Istotnie, zamiast 6 powinno być 7
mp
Ufff. Faktycznie sporo pracy. Niby sam początek łatwy, szybko wpisuje się 5 jako sumę skrajnie prawej kolumny; co nieco daje 7. kolumna, ale potem już żmudnie.
Suma to (+- sumowanie) 36
Noooo, łatwo nie było, zdecydowanie…
Suma to 36
Pozdrawiam 🙂
Usunięte cyfry rzędami od góry: 8,6,3,9,3,3,4,7,7,6,2,3,3,7,6,7.
Suma liczb na przekątnej z dziewięcioma pustymi kratkami =59, na drugiej=39
39 🙂
doskonałe zadanie 🙂 od połowy już z górki, ale istotnie trzeba się było dobrze przyjrzeć i zastanowić 🙂
Pozdrawiam 🙂
Rozwiązanie
http://pokazywarka.pl/4doe5v/
Rozwiązanie znacznie ułatwia fakt, że liczby w diagramie są rozbite na cztery bloki:
2 – elementowy suma 12
3 – elementowy sumy (11,15)
4- elementowy sumy (6,9,8 nieokreslona)
7- elementowy sumy (10,10,9,12,13,14)
Tym sposobem możliwości ustawienia liczb w diagramie jest tylko 84.
Dodatkowym ułatwieniem jest czwarta kolumna od prawej, ponieważ niektóre macki dosięgnąć ją mogą tylko z określonego miejsca.
ciezko bylo, ale sie udalo
http://pokazywarka.pl/lmuzf0/#zdjecie7388453