14 cyfr
Ponad połowa względnie popularnych rodzajów łamigłówek diagramowych polega na wypełnianiu diagramu cyframi. Zwykle kompletnie, czyli żadna kratka nie może pozostać pusta – jak w sudoku, kakuro lub kenkenie. Znacznie mniej liczne i mniej znane są zadania, w których cyfry wskakują tylko do niektórych pól. Takie „niekompletne” przykłady znalazłbym zapewne u klasyków matematyki rozrywkowej, np. w zbiorkach Loyda lub Dudeneya, ale nie chce mi się szperać po bibliotece. Przypomniałem sobie natomiast, że było coś w tym stylu na 12 mistrzostwach świata (Arnhem, 2003), więc wystarczyło sięgnąć po właściwą teczkę.
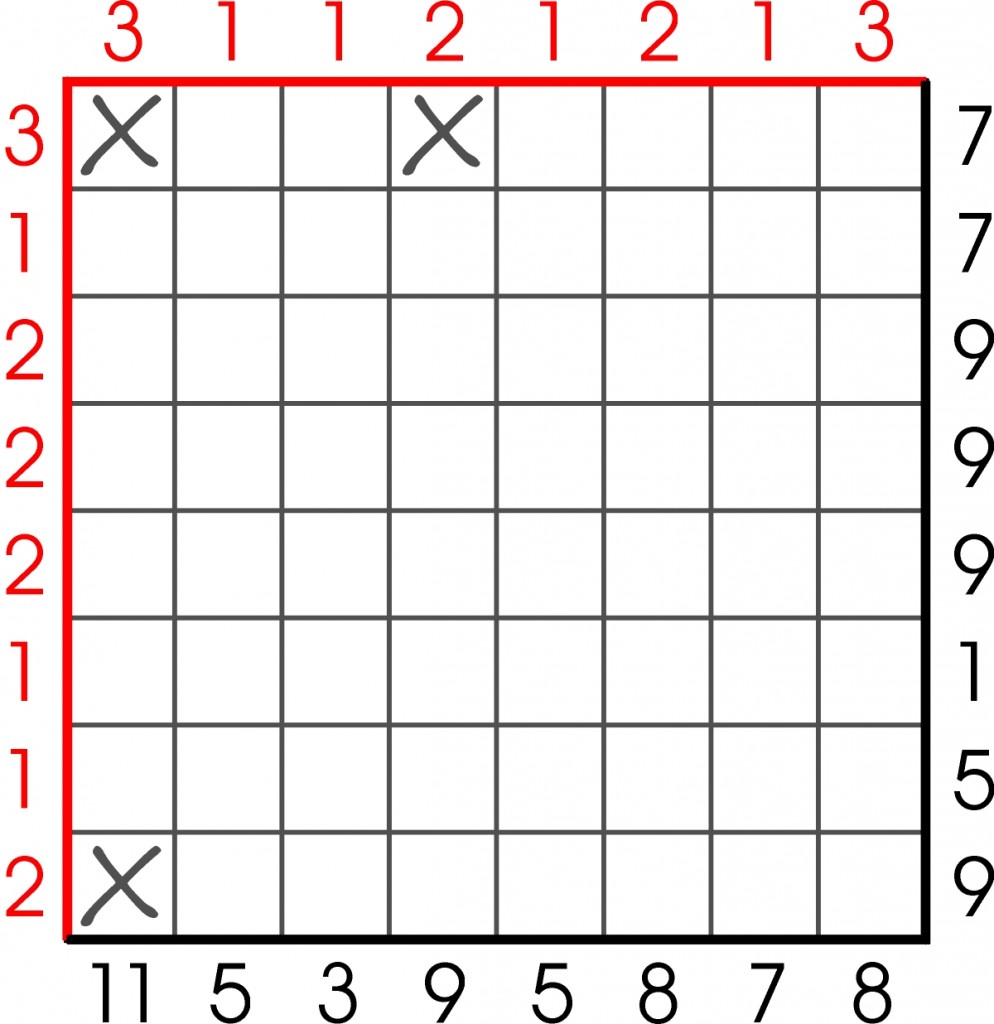
W niektórych kratkach powinny pojawić się cyfry z zakresu od 1 do 9, ale kratki z cyframi nie mogą się ze sobą stykać – nawet rogami. Do przekreślonych pól cyfry na pewno nie trafią.
Czerwone liczby oznaczają, ile cyfr powinno znaleźć się w danym rzędzie (kolumnie), czarne – jaka ma być ich suma.
Zadanie jest wstępem do odmiany macek, o której będzie mowa w następnym wpisie.

Komentarze
Zadanie ma jedno rozwiązanie:
511
7
27
36
45
1
5
27
Pozdrawiam 🙂
Ale tempo!
mp
nie chce być inaczej 😉
http://bankfotek.pl/view/1496381
Rozwiązanie:
http://i.imgur.com/NCPUJJu.png
Pozdrawiam 😉
Odpowiedź skoczkowo-sumowa: (1, 2, 5, 8, 40).
Panie Andrzeju, litości, nie mogę się połapać, na czym polega odpowiedź s-s.
mp
Witam.
Czy wymogiem jest, aby każda liczba z przedziału 1-9 wystąpiła przynajmniej 1?
Nie ma takiego warunku.
mp
x5xxx1x1
xxx7xxxx
2xxxx7xx
xx3xxxx6
4xxx5xxx
xxxxxxx1
5xxxxxxx
xxx2xx7x
X5XXX1X1
XXX7XXXX
2XXXX7XX
XX3XXXX6
4XXX5XXX
XXXXXXX1
5XXXXXXX
XXX2XX7X
drugiego rozgałęzienia:
XX3
7XX
nie sprawdzałem bo skoro jak zwykle ma być tylko jedno rozwiązanie to byłaby to strata czasu 🙂
http://s1.pokazywarka.pl/i/2022842/966829/14-cyfr.jpg
Udało mi się zrozumieć odpowiedź s-s!
Chodzi o sumę liczb z pól osiągalnych trajektorią ruchu jednego skoczka. Żeby posumować wszystkie pola potrzebujemy 5 skoczków, a sumy będą dokładnie takie jak u Andrzeja.
Dodam, że gońcowo-sumowa to: (24,32).
hehe, super odpowiedź Pana Andrzeja 😀 oczywiście wszystko się zgadza a podpowiedź skoczkowo-sumowa mówi wszystko Panie Marku 🙂
Odpowiedź s-s, to sumy pól wyznaczone ruchami skoczka szachowego, gdzie konik szachowy skacze z cyfry na cyfrę. W ten sposób z diagramu można wyodrębnić kilka ścieżek i każdej ścieżce przypisać sumę cyfr znajdujących się na tej drodze.
Diagram po wypełnieniu cyframi wygląda tak:
x5xxx1x1
xxx7xxxx
2xxxx7xx
xx3xxxx6
4xxx5xxx
xxxxxxx1
5xxxxxxx
xxx2xx7x
Ścieżkami konika szachowego na tym diagramie są, np.:
a) 7 (cyfra z najniższego rzędu diagramu) i 1 (trzeci rząd od dołu). Suma tej ścieżki, to: 7+1=8;
b) 2 (cyfra z najniższego rzędu). Suma tej jednopunktowej (z dwójki nie da się skoczyć na inną cyfrę) ścieżki, to: 2.
I tak dalej dla pozostałych ścieżek – c), d), e).
Rozwiązanie
xx3xx3x1
xxx7xxxx
2xxxx7xx
xx3xxxx6
4xxx5xxx
xxxxxxx1
5xxxxxxx
xxx2xx7x
Zadanie przyjemne