Nie tylko kakuro
Zerkając sporadycznie do działu rozrywek umysłowych dziennika Polska zauważyłem z niejakim zdziwieniem, że przynajmniej raz w tygodniu pojawia się w nim kakuro. To chyba ostatni polski bastion medialny tej krzyżówki liczbowej, pomijając parę pisemek specjalistycznych. Właściwie nie powinienem się dziwić, bo Polska jest poniekąd brytyjska, a Wyspiarze zabawy logiczne hołubią, choć akurat w Timesie kakuro nie gości. Jest natomiast stałą pozycją m. in. w The Guardian i Daily Telegraph.
Dziś już mało kto pamięta, że ta łamigłówka miała być następczynią sudoku. Jeszcze w połowie 2005 roku, czyli tuż po zalaniu prasy kwadratami 9×9, angielscy wydawcy zaczęli się rozglądać za kolejnym bakcylem i sięgnęli do źródeł epidemii, czyli do japońskich publikacji dla główkołamaczy. Wybrano to, co było w Japonii popularne i najbardziej krzyżówkowe. W efekcie już we wrześniu 2005 roku z kakuro wystrzelił The Guardian. Potem dołączyło kilka innych dzienników. Początki były obiecujące, nowa moda ruszyła w świat, wydawcy próbowali rozkręcać interes, ale szybko się okazało, że to jednak nie to. Dziś zbiorki z kakuro można kupić na Amazonie za jednego centa.
Pomysł był fajny, ale jednak w praniu bardziej schematyczny niż sudoku, więc szybciej się przejadł, choć z drugiej strony jako lekarstwo na nudę wciąż może być przyjemny i równie skuteczny jak np. zwykłe krzyżówki. Mam oczywiście na myśli zadania starannie opracowane, w których można zmierzać do celu z przyjemnością, jak po nitce do kłębka, dzięki prostej logice i korzystając ewentualnie tylko w niewielkim stopniu z tabelki obejmującej wszystkie możliwe kombinacje liczb tworzących konkretne sumy. Taka tabelka jest w Wikipedii, gdzie nowicjusze znajdą również reguły zabawy. A dla przypomnienia przykład bardzo lekkostrawny – do rozwiązania w głowie.
W przypadku dużych, trudnych zadań, pojawiających się czasem w niektórych mistrzostwach w łamaniu głowy, sztampowość rozwiązywania jest bardziej widoczna i nużąca. Wszystko sprowadza się niemal wyłącznie do prostego algorytmu: wyszukiwania miejsc skrzyżowań dwóch ciągów cyfr (poziomego i pionowego), które mają tylko jedną cyfrę wspólną i wpisywania tej cyfry w pole na skrzyżowaniu.
Warto jeszcze przypomnieć, że kakuro ma tyle wspólnego z Japonią, co sudoku, czyli wywodzi się skądinąd. Japoński wywiad łamigłówkowy podprowadził Amerykanom w latach 80. zadania zwane Cross Sums i zaszczepił je u siebie, skąd via Anglia powróciły do Stanów pod nową nazwą 20 lat później.
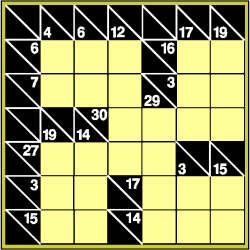
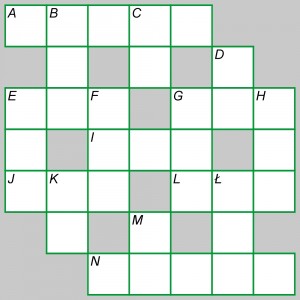
„Znęcam się” nad kakuro w ramach wstępu do wspominków dotyczących innych rodzajów krzyżówek liczbowych, które były popularne przed laty, są mniej schematyczne, a nie mniej ciekawe. Nie chodzi oczywiście o takie krzyżówki, w których w kratki wpisuje się rok bitwy pod Grunwaldem, powierzchnię Polski lub numer telefonu do redakcji. Mam na myśli zadania rachunkowo-logiczne, na przykład takie.
Poziomo:
A) J x F
E) C + Ł
G) D2
I) G poziomo + L
N) C x D x K x M
Pionowo:
B) 3 x E poziomo
C) 1,5 x K
E) B – H
G) iloczyn dwóch liczb pierwszych
H) 2 x Ł
M) D : 2
Osoba, która nadeśle rozwiązanie jako N-ta w kolejności, otrzyma drobny upominek – grę 6. bierze! lub książkę Łamigłówki. Podróże w krainę matematyki rekreacyjnej. N to suma trzech różnych cyfr, które występują najwięcej (tyle samo) razy w rozwiązaniu krzyżówki. Te cyfry wystarczy podać jako rozwiązanie końcowe. Termin nadsyłania rozwiązań, które oczywiście nie będą wcześniej ujawniane – trzy doby od publikacji tego wpisu. Na wszelki wypadek proszę bez figli, czyli jedna osoba = jedno rozwiązanie ![]() .
.

Komentarze
Suma 1+2+7=10. Mam nadzieję, że będę 10-ty (nie chcę być pierwszy !)
Cała krzyżówka
67716xx
x6x8x2x
255×784
9x908x7
114×124
x2x1x3x
xx84672
Panie Marku zaczęły się wakacje, deszcz leje, to może we wpisach zamieszczać po dwie łamigłówki (niekoniecznie szachowe).
????? ?????? ????? ?????? (jak mawiają nasi wschodni sąsiedzi)
Antyp
Takie krzyżówki pojawiały sie dość często w Rozkoszach Łamania Głowy, rubryce łamigłówkowej stworzonej w Życiu Warszawy przez Lecha Pijanowskiego. Czasami miały dodatkowe utrudnienia w postaci nieujawnionej informacji, że liczby są zapisane w układzie innym niż dziesiątkowy.
Witam,
pierwszy raz chciałabym wysłać odpowiedź i dlatego pytam (bo chyba jestem ślepa i nie mogę znaleźć): na jakiego maila?
waruna:
proszę o rozwiązania w komentarzu do wpisu (nie będą ujawnione przed upływem terminu zakończenia zabawy).
m
PS tym razem wyjątkowo nie uwalniam także błędnych rozwiązań.
Pierwszy raz w ogóle komentuję, ale bardzo mi się podobało to zadanie i nawet udało mi się je rozwiązać (chyba). Z mojej krzyżówki wynika, że odpowiedź będzie brzmieć: 1, 2, 7.
Pozdrawiam
1,2,4
P.S. szczerze mówiąc strzelam, a do czego doszedlem to podaję rzędami
A nuż mi się udało 🙂
x,x,x,x,x
_,x,_,x,_,2
2,x,x,_,7,8,4
x,_,9,1,2,_,x
x,x,x,_,1,2,8
_,x,_,1,_,x
_,_,x,4,x,4,x
721
Odpowiedz: 1, 2, 7
Znalazlem po piec cyfr: 1, 2, 7 -> ale nie mam pojecia jak powinna wygladac strategia zglaszania rozwiazan…
Po pięć razy występują cyfry:1,2i7.
Witam
odpowiedź to: 127
Z wielką przyjemnością uporałem się z tym zadaniem po bardzo długim braku kontaktu z tego typu „krzyżówkami”. Bardzo dziękuję Panie Marku za ich przypomnienie.
A = 67716
B = 765
C = 18
D = 28
E(poziomo) = 255
F = 594
G(poziomo) = 784
H = 474
I = 908
J = 114
K = 12
L = 124
Ł = 237
M = 14
N = 84672
E(pionowo) = 291
G(pionowo) = 781
Najczęściej występują cyfry 1, 2, 7 (po 5 razy), stąd N = 10.
67716
_6_8_2
255_784
9_908_7
114_124
_2_1_3
__84672
Rozwiązanie: 10 (1+2+7)
W odróżnieniu od Kakuro, które jednak rozwiązuje się poprzez logiczne rozumowanie, tu trzeba było zacząć od podstawiania kolejnych liczb, żeby znaleźć parę, spełniającą równość G=D^2. Również ostatni związek do wykorzystania czyli A=JxF, gdy znane są dwie pierwsze cyfry J i F, najszybciej rozwiązuje się, podstawiając kolejne cyfry, chociaż pewnie bardziej eleganckie jest spostrzeżenie, że
(110+y)x(590+y)=64900+700y+y^2, a zatem liczba y^2 stanowi dwie ostanie cyfry liczby A
Najwięcej razy występują cyfry: 1,2,7. Każda z nich pojawia się pięciokrotnie.
Zastanawiam się, dlaczego podana została definicja G pionowo? Do rozwiązywania nie jest ona konieczna, a psuje „klimat”, bo jest jedyną definicją słowną wśród pozostałych działań matematycznych.
RoberCie, masz rację. G pionowo to feler. Można z niego skorzystać, ale to tylko dodatkowa droga do celu – zbędna i „toporna”. Inna droga jest nieco dłuższa, ale bardziej elegancka: do okreśłenia G pionowo prowadzi skorzystanie z objaśnienia N poziomo po ustaleniu D i M – najpierw rozszyfrowuje się C i K, co daje ostatnią cyfrę Ł, potem ostatnią cyfrę H i ostatnią I, czyli drugą G pionowo (pierwsza i trzecia „padają” wcześniej)..
m
1, 2, 7.
rozw. – 1,2,7