Tranzytem
Król, skoczek, hetman… Każdym z nich można wykonać ruch w ośmiu kierunkach (oczywiście w sprzyjających okolicznościach), ale dla dwóch pierwszych figur zasięg ruchu jest ściśle określony, natomiast w przypadku hetmana – nie. Zmierzając do celu „królówka” z reguły przemieszcza się „tranzytem” przez inne pola. W związku z tym pojawia się pytanie: czy mijane pola należą do drogi, czy też trasę tworzą tylko te, na których się zatrzymuje?
W klasycznych łamigłówkach, polegających na obchodzeniu szachownicy hetmanem w minimalnej liczbie ruchów, pola przelotowe należą do trasy. W znanym zadaniu Dudeneya z 1906 roku 15 ruchów wystarcza, aby w ten sposób dotrzeć z c3 do f6, zaliczając każde pole, żadnego dwukrotnie:
Gdyby przyjąć, że na trasę składają się tylko pola startowe i końcowe każdego ruchu, to obejście całej szachownicy 8×8 wymagałoby oczywiście 63 ruchów. I tak właśnie jest w hetmańskim hidato.
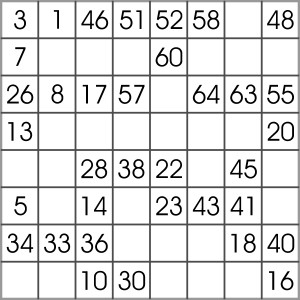
Na diagramie oznaczono numery większości kolejnych pól, na których stawał hetman w trakcie obchodzenia szachownicy. Zadanie polega na ponumerowaniu wolnych pól, pamiętając że:
hetman nigdy nie przechodził tranzytem przez pole, na którym wcześniej się zatrzymał.
Duża liczba ujawnionych liczb jest niestety w tym zadaniu konieczna, aby uniknąć wieloznaczności, choć być może komuś wnikliwemu (Antyp?) uda się bez konsekwencji coś usunąć. Ściślej, konsekwencją może być to, że zadanie zmieni się w mocno nierozrywkowe, choć i tak łatwe nie jest; łatwo można tylko pobłądzić.
W rozwiązaniu wystarczy podać ciąg pięciu liczb wpisanych w dolnym wierszu.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni


Komentarze
Usunąć z tego zadania dodatkowej liczby nie można, raczej należałoby jakąś dołożyć, albowiem zadanie ma co najmniej dwa różne rozwiązania.
03,01,46,51,52,58,47,48
07,02,09,53,60,61,59,54
26,08,17,57,56,64,63,55
13,27,06,50,49,62,19,20
04,12,28,38,22,42,45,21
05,29,14,25,23,43,41,44
34,33,36,24,35,37,18,40
32,11,10,30,15,31,39,16
Łatwo zauważyć, iż 🙂 można zamienić miejscami 42 i 44.
A jednak…
9 jest w złym miejscu, bo w drodze do 10 hetman przechodzi przez 6.
12 jest na trasie 13-14
15 na 30-31
10,11,15,30 na 31-32
24,33 na 34-35
24 na 35-36
itd.
Zapewne niedostatecznie jasno sformułowałem zasady… 🙁
mp
Jakoś tak mi głowa nie „podawała” i ciąg – 4, 9, 11, 25, 24 – został bardziej wymęczony niż znaleziony.
4,31,12,25,11
Błąd: 10 na trasie 30-31
mp
4-9-(10-30)-11-25-24-(16)
Trudne, bo rzeczywiscie bardzo latwo cos przeoczyc.
a
… jak to zwykle bywa, lepiej zacząć od końca, a skończyć na początku…
Dokańczam post bo mi się urwał:
od końca trzeba albo umieszczać kolejna liczbe obok, albo ‚przelatywać’ drogą nad innymi liczbami (juz postawionymi), jak po sznureczku 🙂
Panie Marku, zamiast 14 nie powinno być 11?
Oj poplątało mi sie jak teraz czytam 🙁 nie 11 zamiast 14, ale 12 zamiast 13!
dla jasności dolny rząd wygląda:
4, 35, 10, 30, 24, 25, 9, 16
A tak wogóle to wydaje mi się, że możnaby usunąć chyba tą problematyczną 12/13… chyba…
(kurcze, cały czas myślę, że to jednak ja popełniłem błąd, ale nie mogę go znaleźć i ciągle wychodzi mi, że powinno być tam 12….)
03,01,46,51,52,58,47,48
07,02,50,53,60,59,54,49
26,08,17,57,56,64,63,55
13,27,06,19,39,62,61,20
31,32,28,38,22,44,45,21
05,35,14,37,23,43,41,15
34,33,36,12,29,42,18,40
04,09,10,30,11,25,24,16
Mam pytanie: jaka liczba jest pomiędzy 13 i 14?
Odpowiedź na to i inne pytania w rozwiązaniu jawy piętro wyżej.
mp
Już widzę gdzie sie ‚walnąłem’: przejście między 32 a 33 🙁