Pestki na orzechy
We wpisie z 29 lipca znalazła się następująca pestka:
Spośród liczb:
5, 6, 7, 8, 9, 10
wybrano dwie takie, że:
– różnica ich kwadratów jest sześcianem,
– różnica ich sześcianów jest kwadratem.
Jakie to liczby?
Zadanie jest prostą wyliczanką i ciekawostką liczbowo-retoryczną (sformułowanie dwóch warunków kojarzy się z anastrofą). Jak słusznie zauważył Michał, drugiego warunku mogłoby nie być, ale wtedy nie byłoby ciekawostki. Do niej właśnie nawiązał Esteon, sugerując przerobienie pestki na orzech:
„Ciekawe, na ile to zadanie jest rozwiązywalne w pełnej ogólności, tj. w liczbach naturalnych”.
Chodziłoby więc o szukanie par liczb, których kwadraty różnią się o sześcian, a sześciany o kwadrat, czyli wzorowo:
x^2 – y^2 = a^3
x^3 – y^3 = b^2
Mamy więc układ dwóch równań diofantycznych trzeciego stopnia z czterema niewiadomymi, który jest ciekawy, ale jednak – że tak powiem – rozrywkowy inaczej. Można by próbować przekształcać równania, aby dojść do czegoś „strawnego”, zaczynając np. od wzorów skróconego mnożenia:
(x – y)(x + y) = a^3
(x – y)(x^2 + xy + y^2) = b^2
Dalsza obróbka byłaby jednak tak żmudna, wymagająca wprowadzania tylu podstawień i prowadząca do tak kobylastych wzorów, że ja dziękuję. Prościej i skuteczniej zatrudnić komputer.
Najmniejsza para – (I)[10, 6] – jest rozwiązaniem pestki. Dalej mamy nieskończony ciąg takich par. Oto cztery kolejne:
(II)[640, 384], (III)[7290, 4374], (IV)[8954, 5687], (V)[70434, 64350], …
Dalszych nie znam. Gdyby ktoś poznał, wdzięczny będę za podzielenie się odkryciem. A przy okazji prośba o odpowiedź na pytanie o jeszcze jedną potencjalną ciekawostkę:
Suma i/lub różnica liczb tworzących każdą z pięciu pierwszych par jest kwadratem (dla pierwszych trzech par jest „i„, dla dwóch następnych – „lub„). Czy ta własność jest regułą dla wszystkich par?
Drugą pestkę – tym razem z wpisu z 10 sierpnia – sam zmieniłem w orzech. W łatwym wcieleniu brzmiała tak:
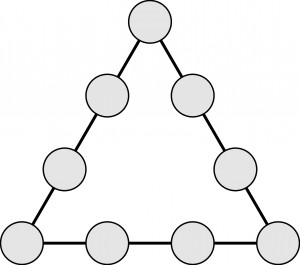
Jeśli do kółek wpisać dziewięć różnych cyfr (od 1 do 9) tak, aby suma czterech liczb na każdym boku trójkąta wynosiła 17, to jakie cyfry znajdą się w narożnych kółkach?
Rozwiązuje się błyskawicznie, bo 51 – 45 = 6 = 1 +2 + 3.
A oto efekt przeróbki, czyli pytanie orzechowe:
Jeśli do kółek wpisać dziewięć różnych cyfr (od 1 do 9) tak, aby suma kwadratów czterech liczb na każdym boku trójkąta była taka sama, to jakie cyfry znajdą się w narożnych kółkach?
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.

Komentarze
Jeśli
x^2 – y^2 = a^3
x^3 – y^3 = b^2
to dla dowolnego naturalnego c mamy:
(x*c^6)^2 – (y*c^6)^2 = c^12*(x^2 – y^2) = (a*c^4)^3
(x*c^6)^3 – (y*c^6)^3 = c^18*(x^3 – y^3) = (b*c^9)^2
Zatem każda para [x,y] generuje nam nieskończenie wiele rozwiązań postaci [x*c^6, y*c^6].
(W ten sposób można wygenerować pary (II) oraz (III) z pary (I) podstawiając c = 2 i c = 3)
Łatwo zauważyć, że wszystkie pary generowane z (I) mają własność „i”, zaś generowane z par (III) oraz (IV) mają własność „lub”.
Osobiście uważam, że NIE wszystkie pary mają tę własność, jednak jedyny sposób, by tego dowieść to znaleźć parę mającą tę własność, czego nie da rady zrobić na piechotę, Z kolei komputery wysiadają już dla liczb 6-cyfrowych.
No chyba, że uda znaleźć się jakąś szybką metodę znajdowania tych par.
Pozdrawiam
Michał
Michale, dzięki za komentarz, po którym – moim zdaniem – temat „liczb zaprzyjaźnionych inaczej” robi się znacznie ciekawszy.
Sprytny wzór dla par, który podałeś, działa wprawdzie wybiórczo, ale dzięki niemu okazało się, że jedna para (między IV a V) mi umknęła – [10n^6, 6n^6] dla n=4, czyli [40960, 24576].
Szkoda, że liczby tak szybko rosną i zabawa w poszukiwanie par staje się praktycznie niemożliwa.
Zdravi
mp
W narożnikach będą cyfry: 2, 5 i 8
Liczby w rogach trojkata – 2, 5, 8.
Suma kwadratow na bokach – 126, suma liczb – 20.
a
Rozwiązanie dla trójkąta
5618
8732
2945