Zakręcone działania

28 stycznia 2008
Marek Penszko

Przedstawiając przed dwoma tygodniami Hexa-Trex wspomniałem, że podobne zadania od lat zamieszczają Japończycy. Właściwie mógłbym to napisać w ciemno, bo w Japonii od dawna trwa taki wysyp różnych rodzajów łamigłówek, że prawdopodobnie nie pozostało już nic oryginalnego do wymyślenia. Zanim więc jakiś atrakcyjny pomysł uznany zostanie za odkrywczy, warto się przedtem upewnić, czy w krainie sake, pachinko i K-1 coś podobnego nie zdążyło już spowszednieć.

Parę lat temu zaskoczyła mnie informacja, że w Japonii działa przynajmniej kilka „Akademii Łamigłówkowych”, których absolwenci zajmują się układaniem zadań publikowanych w prasie lub wydawanych w formie książkowej. Okazało się, że pod dostojną nazwą kryją się zwykle prywatne szkółki albo kursy organizowane przez znanych, cieszących się renomą autorów, ale sam fakt ich istnienia (tzn. „Akademii”, a nie autorów) świadczy o randze rozrywek umysłowych, zwłaszcza logicznych i matematycznych (jest nawet Akademia Matematyki Rekreacyjnej).

Jeden z dalekowschodnich krewniaków Hexa-Trexu, którego nazwę można przetłumaczyć jako Zakręcone działania, należy do grupy kilkuset zadań-przystawek – w przeciwieństwie do kilkudziesięciu dań głównych, do których zalicza się m. in. sudoku, kakuro, filomino i nurikabe. W japońskich magazynach łamigłówkowych poza daniami głównymi i przystawkami jest jeszcze dział debiutancko-eksperymentalny, w którym pojawiają się nowe dania i w zależności od zainteresowania czytelników trafiają do jednej z dwu wspomnianych grup albo zostają uznane za niezbyt smaczne lub ciężkostrawne i wypadają z menu.

W Zakręconych działaniach występuje kilka lub kilkanaście równości z liczbami jedno- i dwucyfrowymi – „połamanych” i wpasowanych w prostokąt. Rozwiązanie polega na ustaleniu granic między nimi i oznaczeniu równości liniami łamanymi. Każda liczba, na której wykonywane jest działanie, znajduje się w jednym polu, czyli nie jest – jak w zadaniu Hexa-Trex – składana z cyfr, jeżeli jest dwucyfrowa. Inna istotna różnica polega na tym, że po ustaleniu kierunku działań należy je wykonywać kolejno, a więc bez uwzględniania pierwszeństwa mnożenia i dzielenia. Poniżej znajduje się przykład z rozwiązaniem oraz zadanie dla bardzo wytrwałych i spostrzegawczych rachmistrzów-kombinatorów.

Zad_1.jpg

 Zad_2.jpg

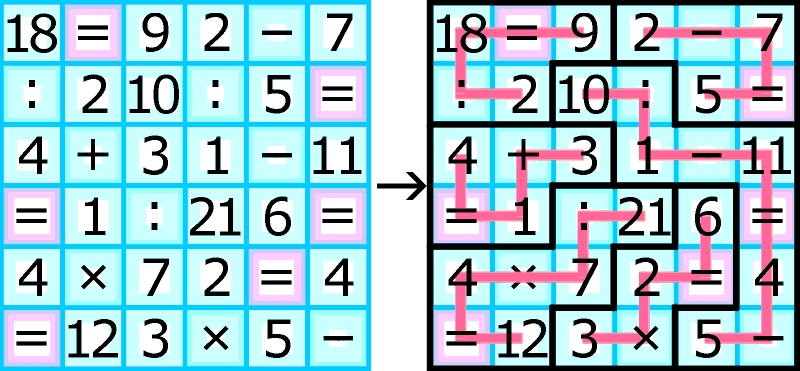
 Jak widać Zakręcone działania są nie tylko dalekowschodnim krewnym Hexa-Trexu, ale w ogóle dalekim, bo obie łamigłówki łączy przede wszystkim ogólna zasada „prostowania” równości, a poza tym sporo dzieli.